Cho các số thực \(a;b;c\)dương thỏa mãn \(a+\sqrt{ab}+\sqrt[3]{abc}=\frac{4}{3}.\)Tìm GTNN của biểu thức \(Z=a+b+c\).
giúp tôi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \({x^2} = 4 = {2^2} = {\left( { - 2} \right)^2} \Leftrightarrow x = \pm 2\)
b) \({x^3} = - 8 = {\left( { - 2} \right)^3} \Leftrightarrow x = - 2.\)
- Chú ý:
Trong toán học, căn bậc chẵn của một số là một số lớn hơn 0. Do đó số âm không có căn bậc chẵn.

Chọn C.
Phương pháp: Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải:


Giả sử phương trình đã cho có 3 nghiệm
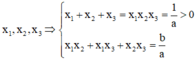
Khi đó
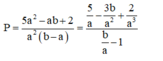
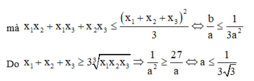
Suy ra
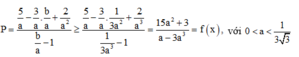
Xét hàm số:
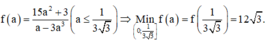
Chọn D.
Ta có \(a+\sqrt{ab}+\sqrt[3]{abc}=\frac{4}{3}\left(a,b,c>0\right)\)
\(\Leftrightarrow4a+4\sqrt{ab}+4\sqrt[3]{abc}=\frac{16}{3}.\)
\(\Leftrightarrow4a+2.2\sqrt{ab}+\sqrt[3]{64abc}=\frac{16}{3}.\)
\(\Leftrightarrow4a+2\sqrt{a.4b}+\sqrt[3]{a.4b.16c}=\frac{16}{3}.\)(1)
Áp dụng BDT Cauchy cho hai số dương \(a\)và \(4b\)ta được:\(2\sqrt{a.4b}\le a+4b\)(dấu bằng có \(\Leftrightarrow a=4b\))(2)
Áp dụng BDT Cauchy cho ba số dương \(a;4b\)và \(16c\)ta được:\(\sqrt[3]{a.4b.16c}\le\frac{1}{3}\left(a+4b+16c\right).\)(dấu bằng có \(\Leftrightarrow a=4b=16c\))(3)
Từ (1);(2) và (3) suy ra:
\(\frac{16}{3}\le4a+a+4b+\frac{1}{3}\left(a+4b+16c\right).\)
\(\Leftrightarrow\frac{16}{3}\le5a+4b+\frac{1}{3}a+\frac{4}{3}b+\frac{16}{3}c.\)
\(\Leftrightarrow\frac{16}{3}\le\frac{16}{3}a+\frac{16}{3}b+\frac{16}{3}c.\)
\(\Leftrightarrow\frac{16}{3}\left(a+b+c\right)\ge\frac{16}{3}.\)
\(\Leftrightarrow a+b+c\ge1\)
\(\Rightarrow MinZ=1\)
\(\Leftrightarrow\hept{\begin{cases}a+\sqrt{ab}+\sqrt[3]{abc}=\frac{4}{3}.\\a+b+c=1\\a=4b=16c\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a=\frac{16}{21}\\b=\frac{4}{21}\\c=\frac{1}{21}\end{cases}}\)
Vậy GTNN của \(Z\)là 1 khi và chỉ khi \(a=\frac{16}{21};b=\frac{4}{21};c=\frac{1}{21}.\)
P/S:Trong quá trình làm dù đã rất cố gắng song khó tránh khỏi sai sót;mong bạn lượng thứ.
Đình chính:
\(MinZ=1\Leftrightarrow\hept{\begin{cases}a+\sqrt{ab}+\sqrt[3]{abc}=\frac{4}{3}\\a=4b=16c\\a+b+c=1\end{cases}\Leftrightarrow\hept{\begin{cases}a=\frac{16}{21}\\b=\frac{4}{21}\\c=\frac{1}{21}\end{cases}}}\)