cho hai đoạn \(A=\left[a;a+2\right]\) và\(B=\left[b;b+1\right]\). Các số a, b thỏa mãn điều kiện gì để \(A\cap B\ne\varnothing\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
a) Ta có:
\(\left. \begin{array}{l}AH \bot \left( P \right)\\BK \bot \left( P \right)\end{array} \right\} \Rightarrow AH\parallel BK\)
Mà \(AB\parallel HK\)
\( \Rightarrow ABKH\) là hình bình hành có \(AH \bot \left( P \right) \Rightarrow AH \bot HK \Rightarrow \widehat {AHK} = {90^ \circ }\)
Vậy \(ABKH\) là hình chữ nhật.
Vậy \(AH = BK\).
b) Ta có:
\(\left. \begin{array}{l}AH \bot \left( Q \right)\\BK \bot \left( Q \right)\end{array} \right\} \Rightarrow AH\parallel BK\)
Mà \(AB\parallel HK\)
\( \Rightarrow ABKH\) là hình bình hành có \(AH \bot \left( Q \right) \Rightarrow AH \bot HK \Rightarrow \widehat {AHK} = {90^ \circ }\)
Vậy \(ABKH\) là hình chữ nhật.
Vậy \(AH = BK\).
BT
23 tháng 9 2016
.
\(A\cap B\ne\varnothing\)khi \(\hept{\begin{cases}b\le a+2\\b+1\ge a\end{cases}\Leftrightarrow\hept{\begin{cases}b-a\le2\\b-a\ge-1\end{cases}}}\Leftrightarrow-1\le b-a\le2.\)
a a+2 b+1 b
CH
Cô Hoàng Huyền
Admin
VIP
23 tháng 9 2016
Ta tìm điều kiện để \(A\cap B=\varnothing\).
Có hai trường hợp :
TH1: \(a+2< b.\)
TH2: \(b+1< a.\)
Để hai trường hợp đều không xảy ra thì \(\hept{\begin{cases}a+2\ge b\\a\le b+1\end{cases}\Rightarrow\hept{\begin{cases}a\ge b-2\\a\le b+1\end{cases}\Rightarrow}b-2\le a\le b+1.}\)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
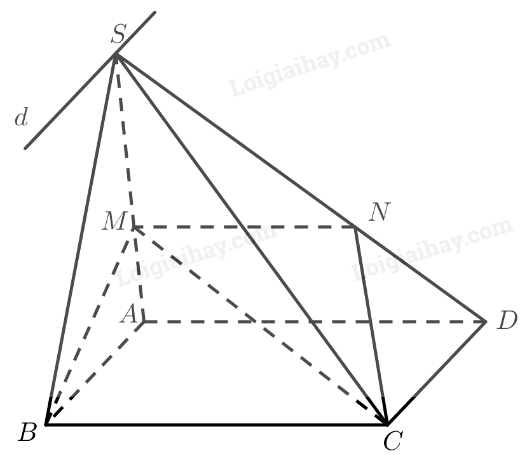
a) Ta có:
\(\left. \begin{array}{l}S \in \left( {SC{\rm{D}}} \right) \cap \left( {SAB} \right)\\C{\rm{D}}\parallel AB\\C{\rm{D}} \subset \left( {SC{\rm{D}}} \right)\\AB \subset \left( {SAB} \right)\end{array} \right\}\)
\( \Rightarrow \)Giao tuyến của hai mặt phẳng \(\left( {SCD} \right)\) và \(\left( {SAB} \right)\) là đường thẳng \(d\) đi qua \(S\), song song với \(C{\rm{D}}\) và \(AB\).
b) Ta có:
\(\begin{array}{l}BC = \left( {BCM} \right) \cap \left( {ABC{\rm{D}}} \right)\\A{\rm{D}} = \left( {SA{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\MN = \left( {BCM} \right) \cap \left( {SA{\rm{D}}} \right)\\BC\parallel A{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(A{\rm{D}}\parallel BC\parallel MN\).
Vậy tứ giác \(CBMN\) là hình thang.
4 tháng 2 2023
Bổ sug đề: Cho (O), BD,CE là các dây của (O)
Sửa đề: Chứng minh góc BOE=góc EDB+góc ECB
1/2(góc EDB+góc ECB)
=1/2(1/2sđ cung EB+1/2sđ cung EB)
=1/2sđ cung EB
=1/2*góc BOE
=>góc EDB+góc ECB=góc BOE
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
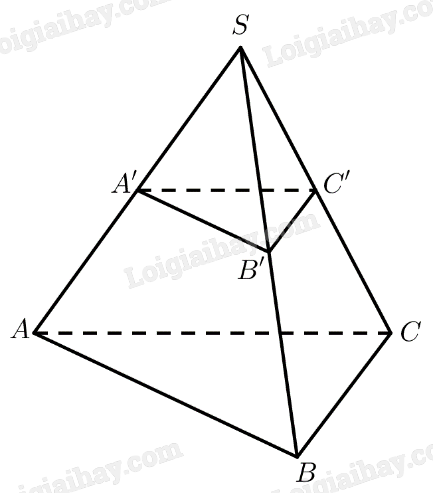
\(A'\) là trung điểm của \(SA\)
\(B'\) là trung điểm của \(SB\)
\( \Rightarrow A'B'\) là đường trung bình của \(\Delta SAB\)
\(\left. \begin{array}{l} \Rightarrow A'B'\parallel AB\\AB \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A'B'\parallel \left( {ABC} \right)\)
\(A'\) là trung điểm của \(SA\)
\(C'\) là trung điểm của \(SC\)
\( \Rightarrow A'C'\) là đường trung bình của \(\Delta SAC\)
\(\left. \begin{array}{l} \Rightarrow A'C'\parallel AC\\AC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A'C'\parallel \left( {ABC} \right)\)
\(\left. \begin{array}{l}A'B'\parallel \left( {ABC} \right)\\A'C'\parallel \left( {ABC} \right)\\A'B',A'C' \subset \left( {A'B'C'} \right)\end{array} \right\} \Rightarrow \left( {A'B'C'} \right)\parallel \left( {ABC} \right)\)
Vậy phần hình chóp đã cho giới hạn bởi hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {A'B'C'} \right)\) là hình chóp cụt đều.
22 tháng 11 2014
a) Điểm B nằm giữa hai điểm A và C
Vì 3cm < 7cm nên AB < AC
b) Vì B nằm giữa hai điểm A và C
Nên AB + BC = AC
Hay 3 + BC = 7
=> BC = 7 – 3 = 4cm
c) Ta có: M là trung điểm của đoạn thẳng BC
=> MB=MC=BC:2=4:2=2cm
9 tháng 12 2017
a, Trên tia Ax có AB < AC ( vì 3cm < 7cm )
nên điểm A nằm giữa 2 điểm B và C
b, Khi đó ta có : BC +AB = AC
\(\Rightarrow\) BC = AC - AB
hay BC = 7 - 3
\(\Rightarrow\) BC = 4 (cm)
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
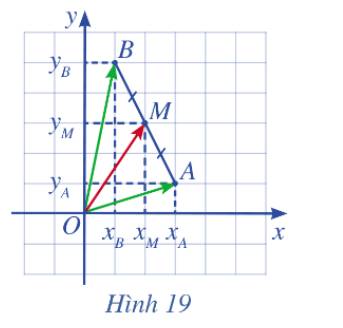
a) Ta có vectơ \(\overrightarrow {OM} \) biểu diễn theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) là: \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) Do tọa độ hai điểm A và B là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\) nên ta có:\(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right)\)
Vậy \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left( {{x_A} + {x_B};{y_A} + {y_B}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm M chính là tọa độ của vectơ nên tọa độ M là \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Ta có \(A\cap B=\varnothing khi\left[{}\begin{matrix}a+2< b\\b+1< a\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a< b-2\\a>b+1\end{matrix}\right.\)
\(\Rightarrow A\cap B\ne\varnothing\) khi \(a\in\left[b-2;b+1\right]\)
A∩B ≠ ∅ \(\Leftrightarrow\left[{}\begin{matrix}a+2\ge b\\b+1\ge a\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a\ge b-2\\b\ge a-1\end{matrix}\right.\)