Cho tứ diện OABC có ba cạnh OA;OB;OC đôi một vuông góc với nhau, . Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC)Tính thể tích khối tứ diện OABH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Gọi M,N lần lượt là trung điểm của BC và OA
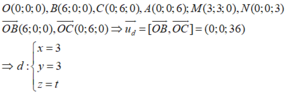
Gọi (P) là mặt phẳng trung trực của OA: z - 3 =0
Goi I là tâm mặt cầu ngoại tiếp tứ diện => I = P ∩ d ⇒ I 3 ; 3 ; 3 R = I A = 3 3

Đáp án D
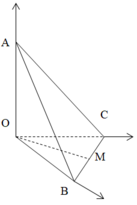
Gọi M,N lần lượt là trung điểm của BC và OA
O ( 0 ; 0 ; 0 ) , B ( 6 ; 0 ; 0 ) , C ( 0 ; 6 ; 0 ) , A ( 0 ; 0 ; 6 ) ; M ( 3 ; 3 ; 0 ) , N ( 0 ; 0 ; 3 ) O B → ( 6 ; 0 ; 0 ) , O C → ( 0 ; 6 ; 0 ) ⇒ u d → = [ O B → , O C → ] = ( 0 ; 0 ; 36 ) ⇒ d : x = 3 y = 3 z = t
Gọi (P) là mặt phẳng trung trực của OA: z - 3 = 0
Goi I là tâm mặt cầu ngoại tiếp tứ diện


Đáp án D
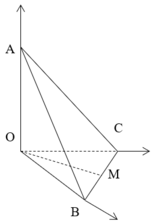
Gọi M, N lần lượt là trung điểm của BC và OA

Gọi (P) là mặt phẳng trung trực của OA: z - 3 = 0
Goi I là tâm mặt cầu ngoại tiếp tứ diện
![]()
R = IA = 3 3

Chọn D

Từ giả thiết suy ra: ΔABC cân tại A có:

Gọi I là trung điểm của BC ⇒ A I ⊥ B C
Giả sử H là trực tâm của tam giác ABC.
Ta thấy O A ⊥ O B C
Vì O B ⊥ O A C ⇒ O B ⊥ A C và A C ⊥ B H nên A C ⊥ O B H ⇒ O H ⊥ A C ( 1 )
B C ⊥ O A I ⇒ O H ⊥ B C ( 2 )
Từ (1) và (2) suy ra O H ⊥ A B C
Có O I = 1 2 B C = a 2 2 = O A
=> ΔAOI vuông cân tại O => H là trung điểm AI và O H = 1 2 A I = a 2
Khi đó:


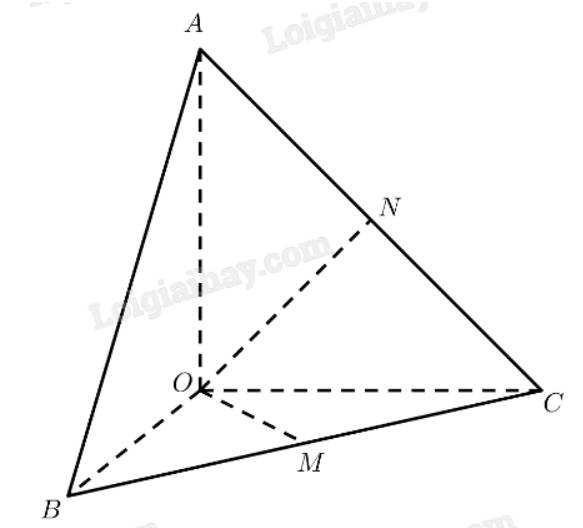
a) Gọi \(M\) là trung điểm của \(BC\).
Tam giác \(OBC\) vuông cân tại \(O \Rightarrow OM \bot BC\)
\(\left. \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OA \bot \left( {OBC} \right) \Rightarrow OA \bot OM\)
\( \Rightarrow d\left( {OA,BC} \right) = OM = \frac{1}{2}BC = \frac{1}{2}\sqrt {O{B^2} + O{C^2}} = \frac{{a\sqrt 2 }}{2}\)
b) Gọi \(N\) là trung điểm của \(AC\).
Tam giác \(OAC\) vuông cân tại \(O \Rightarrow ON \bot AC\)
\(\left. \begin{array}{l}OA \bot OB\\OB \bot OC\end{array} \right\} \Rightarrow OB \bot \left( {OAC} \right) \Rightarrow OB \bot ON\)
\( \Rightarrow d\left( {OB,AC} \right) = ON = \frac{1}{2}AC = \frac{1}{2}\sqrt {O{A^2} + O{C^2}} = \frac{{a\sqrt 2 }}{2}\)

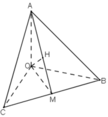
a) Ta có:
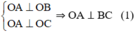
Do H là chân đường vuông góc hạ từ O tới mặt phẳng (ABC) nên:
OH ⊥ (ABC) ⇒ OH ⊥ BC (2)
Mà OA; OH ⊂ (OAH); OA ∩ OH = O (3)
Từ (1); (2) và (3) ⇒ BC ⊥ (OAH)
⇒ BC ⊥ AH
Chứng minh tương tự ta có: AC ⊥ BH
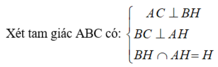
⇒ H là trực tâm ΔABC.
b) Gọi M = AH ∩ BC.
+ BC ⊥ (OAH) ⇒ BC ⊥ OM.
ΔOBC vuông tại O có đường cao OM
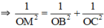
+ OA ⊥ (OBC) ⇒ OA ⊥ OM ⇒ ΔOAM vuông tại O.
OH ⊥ (ABC) ⇒ OH ⊥ AM.
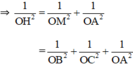
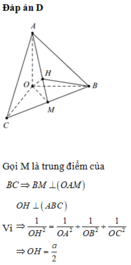

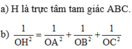

Đáp án D
Gọi M là trung điểm của B C ⇒ B M ⊥ O A M
Vì O H ⊥ A B C ⇒ 1 O H 2 = 1 O A 2 + 1 O B 2 + 1 O C 2 ⇒ O H = a 2
Tam giác OAH vuông tại H, có A H = O A 2 − O H 2 = a 2
Diện tích tam giác vuông OAH là S Δ O A H = 1 2 . O H . A H = a 2 8
Thể tích khối chóp OABH là
V O A B H = 1 3 . B M . S Δ O A H = 1 3 . a 2 2 . a 2 8 = a 3 2 48