a)ΔEAD=ΔECF
B) DE//BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Tính khoảng cách từ B đến d theo t và tìm GTLN của khoảng cách.
- Tìm t và suy ra tọa độ của M.
Cách giải:
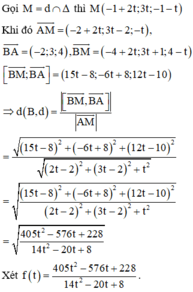
Sử dụng MTCT (chức năng TABLE với bước START nhập -5, bước END nhập 5 và bước STEP nhập 1 ta sẽ được kết quả GTLN f t = 29 tại t = 2)


Xét ΔABD và ΔEBD, ta có:
AB=BE ( gt)
Góc ABD= góc EBD ( Vì BD là tia phân giác của góc B)
BD chung
⇒ΔABD=ΔEBD(c-g-c)
b)Vì ΔABD=ΔEBD nên góc BAD= góc BED=90 độ( 2 cạnh tương ứng)
hay DE vuông góc với BC
c) Vì ΔABD=ΔEBD nên DA=DE ( 2 cạnh tương ứng)
Xét ΔADF và ΔEDC ta có:
góc FAD=góc CED(câu b)
AD=ED (cmt)
góc ADF=gócEDC( đối đỉnh)
⇒ΔADF=ΔEDC (g-c-g)
d,Xét ΔDAE và ΔDCF có:
DA=DC
Góc ADE=góc CDF (đối đỉnh)
DE=DF
⇒ΔDAE = ΔDCF (c-g-c)
⇒góc DAE=góc DCF (2 góc tương ứng)
MÀ 2 góc này ở vị trí SLT
⇒AE//CF
Đúg thì k
Mè sai cx k hộ nhen

a: Ta có: AE+EB=AB
AM+MC=AC
mà AB=AC
và EB=MC
nên AE=AM
hay ΔAEM cân tại A
b: Xét ΔABM và ΔACE có
AB=AC
\(\widehat{BAM}\) chung
AM=AE
Do đó: ΔABM=ΔACE
Suy ra: \(\widehat{ABM}=\widehat{ACE}\)
c: XétΔABC có AE/AB=AM/AC
nên EM//BC

a) Sai
Sửa lại: "Đường thẳng Δ là đường thẳng vuông góc chung của hai đường thẳng chéo nhau a và b nếu Δ cắt cả a và b, đồng thời Δ ⊥ a và Δ ⊥ b"
b) Đúng
c) Đúng
d) Sai
Sửa lại: Đường thẳng đi qua M trên a và vuông góc với a, đồng thời cắt b tại N và vuông góc với b thì đó là đường vuông góc chung của a và b.
e) Sai.
a: Xét ΔEAD và ΔECF có
EA=EC
\(\widehat{AED}=\widehat{CEF}\)(hai góc đối đỉnh)
ED=EF
Do đó: ΔEAD=ΔECF
b: ΔEAD=ΔECF
=>\(\widehat{EAD}=\widehat{ECF}\)
mà hai góc này là hai góc ở vị trí so le trong
nên FC//AD
=>FC//BD
ta có: ΔEAD=ΔECF
=>AD=CF
mà AD=DB
nên CF=DB
Xét ΔDBC và ΔCFD có
DB=CF
\(\widehat{BDC}=\widehat{FCD}\)(hai góc so le trong, BD//FC)
DC chung
Do đó: ΔDBC=ΔCFD
=>\(\widehat{DCB}=\widehat{FDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BC//DF
=>BC//DE
hình tự túc
a) xét △EAD và △ECF, ta có
AE=EC (gt)
DE=EF (gt)
AÊD=FÊC ( đối đỉnh)
=> △EAD= △ECF (c.g.c)
b) ta có △EAD= △ECF (cmt)
=> góc ECF = góc EAD ( góc tương ứng ở vị trí so le trong )
=> DE // BC