Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
\(\Leftrightarrow AH=\dfrac{5\sqrt{15}}{2}\left(cm\right)\)
\(S=\dfrac{\dfrac{5\sqrt{15}}{2}\cdot5}{2}=\dfrac{25\sqrt{15}}{4}\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân

a: Xét ΔANC và ΔAMB có
góc ACN=góc ABM
góc NAC chung
=>ΔANC đồng dạng với ΔAMB

\(cosABC=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}=\dfrac{1}{12}\)
=>góc ABC=85 độ
=>góc ABD=42,5 độ
Xet ΔBAC có BD làphân giác
=>DA/AB=DC/BC
=>DA/6=DC/1=30/7
=>DA=180/7cm
\(cosABD=\dfrac{BA^2+BD^2-AD^2}{2\cdot BA\cdot BD}\)
=>\(\dfrac{30^2+BD^2-\left(\dfrac{180}{7}\right)^2}{2\cdot30\cdot BD}=cos42.5\simeq0,74\)
=>BD^2-11700/49-44.4BD=0
=>\(BD\simeq49,25\left(cm\right)\)

a: Xét ΔAMB và ΔAMC có
AB=AC
góc BAM=góc CAM
AM chung
=>ΔAMB=ΔACM
b:
ΔABC cân tại A có AM là phân giác
nên AM vuông góc BC và M là trung điểm của BC
MB=MC=BC/2=3cm
=>AM =căn 5^2-3^2=4cm
c: Xét ΔMHB vuông tại H và ΔMKC vuông tại K có
MB=MC
góc B=góc C
=>ΔMHB=ΔMKC
=>MH=MK
Xét ΔHMQ vuông tại H và ΔKMP vuôg tại K có
MH=MK
góc HMQ=góc KMP
=>ΔHMQ=ΔKMP
=>MQ=MP
=>ΔMQP cân tại M

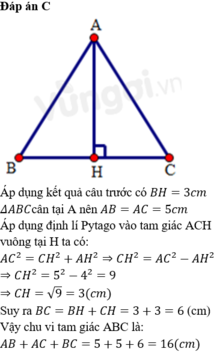
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC và AH là phân giác của góc BAC
=>HB=HC
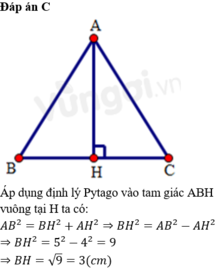
b: HB=HC=3cm
=>AH=4cm
AH là phân giác của góc BAC
=>góc BAH=góc CAH
c: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
góc MAH=góc NAH
=>ΔAMH=ΔANH
=>HM=HN
=>ΔHMN cân tại H
a) Ta có: ΔABC cân tại A(gt)
mà AM là đường trung tuyến ứng với cạnh đáy BC(M là trung điểm của BC)
nên AM là đường cao ứng với cạnh BC(Định lí tam giác cân)
⇒AM⊥BC(đpcm)
Ta có: M là trung điểm của BC(gt)
nên \(BM=MC=\dfrac{BC}{2}=\dfrac{6}{2}=3\left(cm\right)\)
Áp dụng định lí pytago vào ΔABM vuông tại M, ta được:
\(AB^2=AM^2+MB^2\)
\(\Leftrightarrow AM^2=AB^2-MB^2=5^2-3^2=16\)
hay AM=4(cm)
Vậy: AM=4cm
b) Ta có: AI+IB=AB(I nằm giữa A và B)
AJ+JC=AC(J nằm giữa A và C)
mà AB=AC(ΔABC cân tại A)
và AI=AJ(gt)
nên BI=CJ(đpcm)