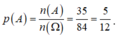Cho tập hợp S = {1;2;3;4;5;6;7;8;9}. Chọn ngẫu nhiên ba số từ tập S. Tính xác suất của biến cố trong ba số được chọn ra không chứa hai số nguyên liên tiếp nào.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: A
S chỉ có 1 tập con
⇔ S = ∅ ⇔ (m - 1; m + 1) ⊂ (-∞; 1].
⇔ m + 1 ≤ 1 ⇔ m ≤ 0

Để \(x=\frac{a-20}{-3}\) ( a ∈ N* ) nhận giá trị dương
=> a - 20 nhận giá trị âm
=> a nhỏ hơn 20
a) S = { a ∈ N* | a < 20 }
\(S=\left\{...;17;18;19\right\}\)
b) ( Không hiểu đề , thông cảm , bạn làm nốt nhé ! )

Chọn A
Cách 1.
Giả sử ![]() Đặt
Đặt ![]() Khi đó
C
1
,
C
2
, C là ba tập con không giao nhau của S và S =
C
1
∪
C
2
∪
C
Khi đó
C
1
,
C
2
, C là ba tập con không giao nhau của S và S =
C
1
∪
C
2
∪
C
Khi đó mỗi phần tử x ∈ S có 3 khả năng: Hoặc thuộc tập C 1 hoặc thuộc tập C 2 hoặc thuộc tập C.
Do đó 12 phần tử sẽ có 3 12 cách chọn.
Trong các cách chọn nói trên có 1 trường hợp C 1 = C 2 = ∅ , C = S
Các trường hợp còn lại thì lặp lại 2 lần (đổi vai trò C 1 và C 2 cho nhau).
Do đó số cách chia là 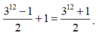
Cách 2.
Đặt S = S 1 ∪ S 2
Nếu
S
1
có k phần tử ![]()
![]()
![]()
![]()
Vậy số cách chọn 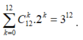
Nhưng trường hợp ![]() giống nhau và không hoán vị nên có
giống nhau và không hoán vị nên có  cách
cách

Tập hợp S có số phần tử là:
(166-6) : 4=40 (phần tử)
Cách làm đơn giản thế này thôi bạn nhé! Chúc bạn học tốt.
Chọn D
Xét phép thử: “Chọn ngẫu nhiên ba số từ tập S = {1;2;3;4;5;6;7;8;9}. Ta có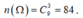 .
.
Gọi A là biến cố: “trong ba số được chọn ra không chứa hai số nguyên liên tiếp”.
Gọi a 1 , a 2 , a 3 là ba số thỏa mãn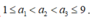 .
.
Không có hai số nguyên liên tiếp nào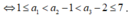 .
.
Đặt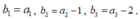 . Khi đó:
. Khi đó: 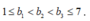 .
.
Số cách chọn bộ ba số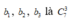 => có
C
7
3
cách chọn
a
1
,
a
2
,
a
3
=> có
C
7
3
cách chọn
a
1
,
a
2
,
a
3
Suy ra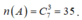
Do đó