Cho hàm số (m là tham số thực) thỏa mãn Mệnh đề nào dưới đây đúng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Đạo hàm f'(x) = 1 - m ( x + 1 ) 2 .
+ Suy ra hàm số f(x) là hàm số đơn điệu trên đoạn [1; 2] với mọi m≠ 1.
+ Khi đó ta có :
m i n y [ 1 ; 2 ] + m a x [ 1 ; 2 ] y = f ( 1 ) + f ( 2 ) = m + 1 2 + m + 2 3 = 16 3 ↔ 5 m 6 = 25 6 ↔ m = 5
Chọn D.

Đáp án C
Phương pháp: Hàm số bậc nhất trên bậc nhất y = a x + b c x + d a d - b c ≠ 0 luôn đơn điệu trên từng khoảng xác định của nó.
TH1: Hàm số đồng biến trên [2;4] => m a x 2 ; 4 y = y ( 4 )
TH2: Hàm số nghịch biến trên [2;4] => m a x 2 ; 4 y = y ( 2 )
Cách giải: Tập xác định: D = R\{1}
Ta có: 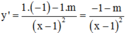
TH1: ![]()
![]() =>Hàm số đồng biến trên
=>Hàm số đồng biến trên 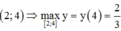
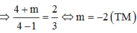
TH2: ![]()
![]() => Hàm số nghịch biến trên
=> Hàm số nghịch biến trên ![]()
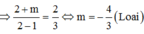
Vậy m = –2
Dựa vào các đáp án ta thấy chỉ có đáp án C thỏa mãn



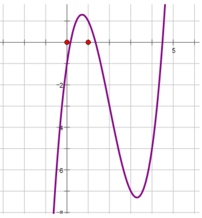
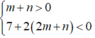 .Tìm số cực trị của hàm số
.Tìm số cực trị của hàm số







Đáp án C
Ta có: y ' = − 1 − m x − 1 2
· Trường hợp 1: nếu y ' > 0 ⇒ m < − 1 , lúc này hàm số đồng biến
⇒ min 2 ; 4 y = y 2 = 2 + m 2 − 1 = 3 ⇒ m = 1 (mâu thuẫn với m < -1) => loại
· Trường hợp 2: nếu y ' < 0 ⇒ m > − 1 , lúc này hàm số nghịch biến
⇒ min 2 ; 4 y = y 4 = 4 + m 4 − 1 = 3 ⇒ m = 5 (thỏa mãn với m > -1) => chọn
Đối chiếu 4 đáp án thì có đáp án C là thỏa mãn.