Trong không gian Oxyz, cho tam giác ABC với A(-1;0;2), B(1;2;-1), C(-3;1;2). Mặt phẳng (P) đi qua trọng tâm của tam giác ABC và vuông góc với đường thẳng AB là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

CM
9 tháng 2 2019

Một VTCP của đường phân giác trong góc A của tam giác ABC là
![]()
Phương trình đường phân giác góc A là
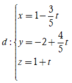
Suy ra đường thẳng d cắt mặt phẳng (Oyz) tại ![]()
Chọn C.

CM
26 tháng 7 2019
Đáp án A
Gọi D là chân đường phân giác góc B của tam giác ABC . Theo tính chất đường phân giác ta có : 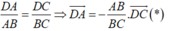
![]()
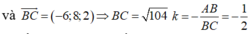
Từ (*) ta có, điểm D chia đoạn thẳng AC theo tỷ số k nên D có toạ độ
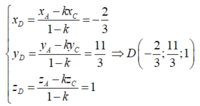
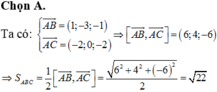

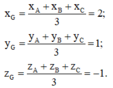

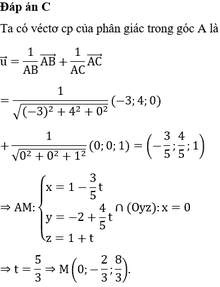
Đáp án B
Phương pháp: - Trọng tâm G của tam giác ABC có tọa độ được tính:
- Phương trình mặt phẳng đi qua M x 0 ; y 0 ; z 0 và có 1 VTPT n → =(a;b;c)
Cách giải: Trọng tâm G của tam giác ABC: G(-1;1;1)
(P) vuông góc với AB => (P) nhận A B → = ( 2 ; 2 ; - 3 ) là một VTPT
Phương trình mặt phẳng (P):