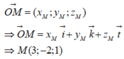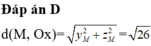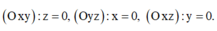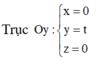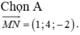Trong không gian Oxyz, cho điểm M(2;0;1). Gọi A, B lần lượt là hình chiếu của M trên trục Ox và trên mặt phẳng (Oyz). Viết phương trình mặt trung trực của đoạn AB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn B
Gọi M (x; y; z)
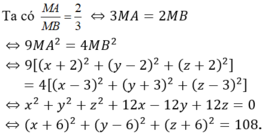
Như vậy, điểm M thuộc mặt cầu (S) tâm I(-6;6;-6) và bán kính R = √108 = 6√3. Do đó OM lớn nhất bằng
![]()

Đáp án D
Phương pháp: (Oxy): z = 0, (Oyz): x = 0, (Oxz): y = 0
Trục Oy: x = 0 y = t z = 0
Cách giải: M (1;0;3) ∈ (Oxz)

Đáp án C
Vecto đơn vị trong hệ trục Oxyz: ![]()
Tọa độ điểm M trong không gian Oxyz: ![]()
Cách giải