trên mặt phẳng tọa độ Oxy, cho tam giác ABC cóA(2;1). Gọi M,N lần lượt là trung điểm của đt AB và AC biết BN: x-2y+4=0, CM: 2x+y-6=0. tìm tọa độ của B và C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi B',C' lần lượt là chân đường phân giác kẻ từ B,C xuống lần lượt AC,AB
GỌi i là giao của BB' và CC'
Tọa độ I là:
x-1=0 và x-y-1=0
=>x=1 và y=0
Kẻ IH vuông góc AC tại H
=>H(2;-3)
=>vecto AH=(-2;-2)=(1;1)
Phương trình AH là:
1(x-4)+1(y+1)=0
=>x+y-3=0
=>AC: x+y-3=0
Tọa độ C là:
x+y-3=0 và x-y-1=0
=>C(2;1)

Do C thuộc Ox nên tọa độ có dạng: \(C\left(x;0\right)\)
Do trọng tâm G thuộc Oy \(\Rightarrow x_G=0\)
Mà \(x_A+x_B+x_C=3x_G\)
\(\Rightarrow1+\left(-3\right)+x=3.0\)
\(\Rightarrow x=2\)
\(\Rightarrow C\left(2;0\right)\)

\(\overrightarrow{AB}=\left(-3;-2\right)\)
\(\overrightarrow{AC}=\left(-1;0\right)\)
\(\overrightarrow{AB}+\overrightarrow{AC}=\left(-4;-2\right)\)

Gọi I(a; b) là tâm đường tròn ngoại tiếp tam giác ABC.
A I 2 = B I 2 A I 2 = C I 2 ⇔ a − 0 2 + b − 2 2 = a + 2 2 + b − 8 2 a − 0 2 + b − 2 2 = a + 3 2 + b − 1 2
⇔ a 2 + b 2 − 4 b + 4 = a 2 + 4 a + 4 + b 2 − 16 b + 64 a 2 + b 2 − 4 b + 4 = a 2 + 6 a + 9 + b 2 − 2 b + 1
4 a − 12 b = − 64 6 a + 2 b = − 6 ⇔ a − 3 b = − 16 3 a + b = − 3
⇔ a = − 5 2 b = 9 2
Chọn B.

vecto AH=(x+2;y-4); vecto BC=(-6;-2)
vecto BH=(x-4;y-1); vecto AC=(0;-5)
Theo đề, ta có: -6(x+2)-2(y-4)=0 và 0(x-4)-5(y-1)=0
=>y=1 và -6(x+2)=2(y-4)=2*(1-4)=-6
=>x+2=1 và y=1
=>x=-1 và y=1

AB (-1,-3)
AC (3,1)
BC (4.4)
Ta co : AB.AC= (-1).(3) + (-3).(1) = 0
suy ra : tam giac ABC vuong tai A
S= 1/2.AB.AC
Ban tu tinh do dai AB, AC nhé

Gọi I( x; y). Ta có A I → = x + 4 ; y − 1 B I → = x − 2 ; y − 4 C I → = x − 2 ; y + 2 .
Do I là tâm đường tròn ngoại tiếp tam giác ABC nên I A = I B = I C ⇔ I A 2 = I B 2 I B 2 = I C 2
⇔ x + 4 2 + y − 1 2 = x − 2 2 + y − 4 2 x − 2 2 + y − 4 2 = x − 2 2 + y + 2 2 ⇔ x + 4 2 + y − 1 2 = x − 2 2 + y − 4 2 y − 4 2 = y + 2 2 ⇔ x + 4 2 = x − 2 2 + ( 1 − 4 ) 2 y = 1 ⇔ x 2 + 8 x + 16 = x 2 − 4 x + 4 + 9 y = 1 ⇔ x = − 1 4 y = 1 .
Chọn B.

Gọi \(C\left(x;0\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-6;2\right)\\\overrightarrow{BC}=\left(x+2;-4\right)\end{matrix}\right.\)
Tam giác ABC vuông tại B \(\Leftrightarrow\overrightarrow{AB}.\overrightarrow{BC}=0\)
\(\Rightarrow-6\left(x+2\right)-8=0\) \(\Rightarrow x=-\dfrac{10}{3}\)
\(\Rightarrow C\left(-\dfrac{10}{3};0\right)\)
Bạn tự tính tọa độ \(\overrightarrow{AC};\overrightarrow{BC}\) từ đó suy ra độ dài 3 cạnh và tính được chu vi, diện tích
Do tam giác ABC vuông tại B nên ABCD là hcn khi \(\overrightarrow{AB}=\overrightarrow{DC}\)
Gọi \(D\left(x;y\right)\Rightarrow\overrightarrow{DC}=\left(-\dfrac{10}{3}-x;-y\right)\)
\(\Rightarrow\left\{{}\begin{matrix}-\dfrac{10}{3}-x=-6\\-y=2\end{matrix}\right.\) \(\Rightarrow D\left(\dfrac{8}{3};-2\right)\)
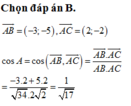
Gọi G là trọng tâm tam giác \(\Rightarrow\) tọa độ G là nghiệm
\(\left\{{}\begin{matrix}x-2y+4=0\\2x+y-6=0\end{matrix}\right.\) \(\Rightarrow G\left(\frac{8}{5};\frac{14}{5}\right)\)
Gọi P là trung điểm BC, theo tính chất trọng tâm: \(\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AP}\Rightarrow P\left(\frac{7}{5};\frac{37}{10}\right)\)
Gọi \(M\left(a;-2a+6\right)\) \(\Rightarrow\left\{{}\begin{matrix}x_B=2x_M-x_A=2a-2\\y_B=2y_M-y_A=-4a+11\end{matrix}\right.\)
P là trung điểm BC \(\Rightarrow\left\{{}\begin{matrix}x_C=2x_P-x_B=\frac{24}{5}-2a\\y_C=2y_P-y_B=4a-\frac{18}{5}\end{matrix}\right.\)
N là trung điểm AC \(\Rightarrow\left\{{}\begin{matrix}x_N=\frac{x_A+x_C}{2}=\frac{17}{5}-a\\y_N=\frac{y_A+y_C}{2}=2a-\frac{13}{10}\end{matrix}\right.\)
Do N thuộc BN nên:
\(\frac{17}{5}-a-2\left(2a-\frac{13}{10}\right)+4=0\) \(\Rightarrow a=2\)
\(\Rightarrow\left\{{}\begin{matrix}B\left(2;3\right)\\C\left(\frac{4}{5};\frac{22}{5}\right)\end{matrix}\right.\)