Trong không gian Oxyz,viết phương trình đường thẳng d qua M(3;2;-5) và vuông góc với mặt phẳng (P): x-2y-5z+1=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Mặt phẳng (P) có vecto pháp tuyến là: n p → (3; 1; 0)
Vì đường thẳng d vuông góc với mặt phẳng (P) nên đường thẳng d có vecto chỉ phương là: u d → = n p → (3; 1; 0)
Phương trình tham số của đường thẳng d:
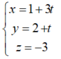
Chọn D.

Đáp án D
Gọi H là hình chiếu của A trên đường thẳng d.
Ta có: AH ≤ AM nên khoảng cách từ A đến đường thẳng d nhỏ nhất khi AH trùng với mới AM, khi đó H trùng với M và AM vuông góc d. Mặt phẳng (P) có vecto pháp tuyến n p → (1; 1; 1) . AM → (0; -2; -1) Đường thẳng d nhận vecto [ AM → ; n p → ] làm vecto chỉ phương. Phương trình tham số của d:

Dưới đây là hướng dẫn chi tiết giải bài toán từ link bạn cung cấp:
Đề bài
Trong không gian Oxyz, cho hai điểm \(A \left(\right. 3 ; 2 ; 1 \left.\right)\), \(M \left(\right. 3 ; 0 ; 0 \left.\right)\) và mặt phẳng \(\left(\right. P \left.\right) : x + y + z - 3 = 0\).
Viết phương trình của đường thẳng \(d\) đi qua điểm \(M\), nằm trong mặt phẳng \(\left(\right. P \left.\right)\) sao cho khoảng cách từ \(A\) đến đường thẳng \(d\) nhỏ nhất.
Phân tích & Cách giải
1. Điều kiện của đường thẳng \(d\)
- Đi qua \(M \left(\right. 3 ; 0 ; 0 \left.\right)\).
- Nằm trong mặt phẳng \(\left(\right. P \left.\right)\).
- Khoảng cách từ \(A\) đến \(d\) nhỏ nhất.
2. Nhận xét quan trọng
Khoảng cách từ \(A\) đến \(d\) nhỏ nhất khi đường thẳng \(d\) nằm trong \(\left(\right. P \left.\right)\), đi qua \(M\) và vuông góc với đoạn \(A M\).
3. Tìm vector chỉ phương của \(d\)
- \(\overset{\rightarrow}{A M} = \left(\right. 3 - 3 , 0 - 2 , 0 - 1 \left.\right) = \left(\right. 0 , - 2 , - 1 \left.\right)\)
- Đường thẳng \(d\) nằm trong \(\left(\right. P \left.\right)\) nên vector chỉ phương \(\overset{\rightarrow}{u}\) của \(d\) phải vuông góc với vector pháp tuyến của \(\left(\right. P \left.\right)\): \(\overset{\rightarrow}{n_{P}} = \left(\right. 1 , 1 , 1 \left.\right)\)
- Đồng thời, \(\overset{\rightarrow}{u}\) phải vuông góc với \(\overset{\rightarrow}{A M}\)
Vậy:
\(\overset{\rightarrow}{u} = \overset{\rightarrow}{A M} \times \overset{\rightarrow}{n_{P}}\)
Tính tích có hướng:
\(\overset{\rightarrow}{u} = \mid \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 0 & - 2 & - 1 \\ 1 & 1 & 1 \mid = \mathbf{i} \left(\right. \left(\right. - 2 \left.\right) \cdot 1 - \left(\right. - 1 \left.\right) \cdot 1 \left.\right) - \mathbf{j} \left(\right. 0 \cdot 1 - \left(\right. - 1 \left.\right) \cdot 1 \left.\right) + \mathbf{k} \left(\right. 0 \cdot 1 - \left(\right. - 2 \left.\right) \cdot 1 \left.\right)\) \(= \mathbf{i} \left(\right. - 2 + 1 \left.\right) - \mathbf{j} \left(\right. 0 + 1 \left.\right) + \mathbf{k} \left(\right. 0 + 2 \left.\right) = \mathbf{i} \left(\right. - 1 \left.\right) - \mathbf{j} \left(\right. 1 \left.\right) + \mathbf{k} \left(\right. 2 \left.\right)\) \(\Rightarrow \overset{\rightarrow}{u} = \left(\right. - 1 , - 1 , 2 \left.\right)\)4. Viết phương trình tham số của \(d\)
Đường thẳng \(d\) đi qua \(M \left(\right. 3 ; 0 ; 0 \left.\right)\), nhận \(\overset{\rightarrow}{u} = \left(\right. - 1 , - 1 , 2 \left.\right)\) làm vector chỉ phương:
\(\boxed{\left{\right. x = 3 - t \\ y = 0 - t \\ z = 0 + 2 t \left(\right. t \in \mathbb{R} \left.\right)}\)Hoặc:
\(\boxed{\frac{x - 3}{- 1} = \frac{y}{- 1} = \frac{z}{2}}\)Kết luận
Phương trình đường thẳng \(d\) cần tìm là:
\(\boxed{\frac{x - 3}{- 1} = \frac{y}{- 1} = \frac{z}{2}}\)hoặc
\(\boxed{\left{\right. x = 3 - t \\ y = - t \\ z = 2 t}\)Nếu bạn cần giải thích thêm về các bước giải hoặc muốn biết cách tính khoảng cách, hãy hỏi nhé!

Ta có: a d → = (2; −1; 4)
Xét điểm B(–3 + 2t; 1 – t; –1 + 4t) thì AB → = (1 + 2t; 3 − t; −5 + 4t)
AB ⊥ d ⇔ AB → . a d → = 0
⇔ 2(1 + 2t) − (3 − t) + 4(−5 + 4t) = 0 ⇔ t = 1
Suy ra AB → = (3; 2; −1)
Vậy phương trình của
∆
là 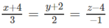

Đáp án A
Đường thẳng d đi qua điểm M(-1;0;0) và có một véc-tơ chỉ phương là ![]() =(1;2;-1) nên d có phương trình chính tắc là
=(1;2;-1) nên d có phương trình chính tắc là 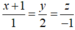

Đáp án D
∆ có véc tơ chỉ phương là u → = 2 ; 1 - 1 . Gọi N là giao điểm của d và ∆ ⇒ N 2 t + 1 ; t - 1 ; - t
Theo đề bài ta sẽ có: u → . M N → = 0 ⇔ t = 2 3 ⇒ M N → = 1 3 ; - 4 3 ; - 2 3 ⇒ d : x - 2 1 = y - 1 - 4 = z - 2

Chọn đáp án D
Ta thấy điểm M(3;-3;-6) không thuộc d.
Thật vậy, với giả thiết đề bài cho thì đường thẳng d có phương trình tham số là

Do đó phương trình ở đáp án D không phải là phương trình của d.
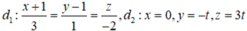


d : x = 3 + t y = 2 - 2 t z = - 5 - 5 t
Đáp án D