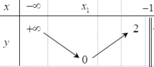
Cho hàm số y = f(x) xác định trên khoảng (-2;-1) và có . Hỏi khẳng định nào dưới đây là khẳng định đúng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
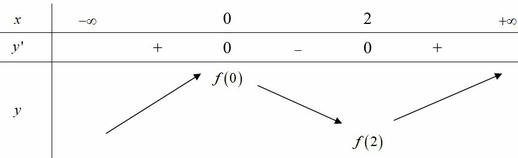
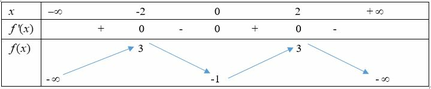
Dựa vào đồ thị hàm số f ' ( x ) suy ra BBT của hàm số y = f(x)

Khẳng định 1, 2, 5 đúng, khẳng định 4 sai.
Xét khẳng định 3: Ta có:
f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) ⇒ f ( 3 ) - f ( 0 ) = f ( 1 ) - f ( 2 ) > 0
Do đó f ( 3 ) > f ( 0 ) ⇒ Vậy khẳng định 3 đúng.

Đáp án A
Điều kiện đủ để hàm số y=f(x) đồng biến trên k là f ' x > 0 với mọi x ∈ K . Đáp án D thiếu tại hữu hạn điểm thuộc khoảng K.

Đáp án A
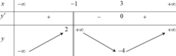
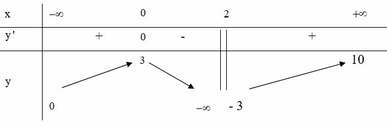
Từ bảng biến thiên của hàm số y=f(x), suy ra bảng biến thiên của hàm số y = f ( x ) là

Dựa vào bảng biến thiên, ta suy ra hàm số có 4 điểm cực trị.

Đáp án D
Ta có Đáp án D
Ta có y’ = –f’(1 – x) + 2018 = –[1–(1–x)][(1–x)+2]g(1–x) – 2018 + 2018
= –x(3–x)g(1–x)
Suy ra 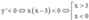 (vì g(1–x) < 0,
∀
x
∈
R
)
(vì g(1–x) < 0,
∀
x
∈
R
)
Vậy hàm số đã cho nghịch biến trên khoảng 3 ; + ∞







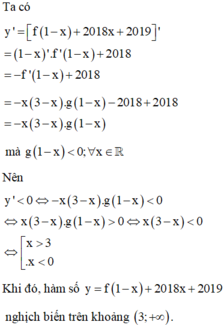

Đáp án C
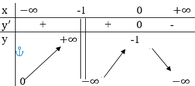
lim x → 2 - f ( x ) = 2 , lim x → 1 - f ( x ) = - ∞ nên đồ thị hàm số có duy nhất 1 đường tiệm cận đứng là x = -1