Cho tam giác ABC biết các cạnh a = 52, 1cm; b = 85cm và c = 54cm. Tính các góc
#Hỏi cộng đồng OLM
#Toán lớp 10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: \(BH=\dfrac{5\sqrt{3}}{3}\left(cm\right)\)
a: Đề sai rồi bạn
a.=> BC = BH + CH = 1 + 3 = 4 cm
áp dụng định lý pitago vào tam giác vuông AHB
\(AB^2=HB^2+AH^2\)
\(AB=\sqrt{1^2+2^2}=\sqrt{5}cm\)
áp dụng định lí pitago vào tam giác vuông AHC
\(AC^2=AH^2+HC^2\)
\(AC=\sqrt{2^2+3^2}=\sqrt{13}cm\)

a, Theo định lí Pytago tam giác ABH vuông tại H
\(AB=\sqrt{BH^2+AH^2}=\sqrt{5}cm\)
Theo định lí Pytago tam giác AHC vuông tại H
\(AC=\sqrt{AH^2+HC^2}=\sqrt{4+9}=\sqrt{13}\)cm
-> BC = HB + HC = 4 cm
b, Ta có tam giacs ABC đều mà BH là đường cao hay BH đồng thời là đường trung tuyến
=> AH = AC/2 = 5/2
Theo định lí Pytago tam giác ABH vuông tại H
\(BH=\sqrt{AB^2-AH^2}=\dfrac{5\sqrt{3}}{2}cm\)

Theo bất đẳng thức tam giác ABC ta có:
\(AC – BC < AB < AC + BC \)
Thay BC = 1cm, AC = 7cm, ta được:
\(7 – 1 < AB < 7 + 1\)
\(6 < AB < 8 (1)\)
Vì độ dài AB là một số nguyên (cm) thỏa mãn (1) nên AB = 7cm
Do đó ΔABC cân tại A vì AB = AC = 7cm.
tham khảo:

a) Xét tam giác ABH vuông tại H. Áp dụng định lý Pi-ta-go trong tam giác vuông ta có:
BH2+AH2=AB2
<=> 1+4=5(cm)
<=> AB=\(\sqrt{5}\)cm
Xét tam giác AHC vuông tại H. Áp dụng định lí Pi-ta-go ta có:
HC2+AH2=AC2
<=> 9+4=13(cm)
<=> AC=\(\sqrt{13}\left(cm\right)\)
Xét BC=BH+HC=1+3=4(cm)
b) Áp dụng công thức tính đường cao trong tam giác đều, ta có:
BH=\(5\cdot\frac{\sqrt{3}}{2}=\frac{5\sqrt{3}}{2}\)
Từ định lí cosin a2 = b2 + c2 – 2bc. cosA
ta suy ra cos A =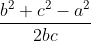 =
= 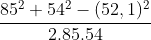
=> cosA ≈ 0,8089 =>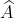 = 360
= 360
Tương tự, ta tính được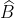 ≈ 1060 28’ ;
≈ 1060 28’ ; 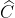 ≈ 370 32’.
≈ 370 32’.