a,b là số thực ; a^2+b^2 <= a+b . Tìm Max (a+2b)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
a) Mệnh đề có dạng \(P \Rightarrow Q\) với P: “\(2a - 1 > 0\)” và Q: “\(a > 0\)”
Ta thấy khi P đúng (tức là \(a > \frac{1}{2}\)) thì Q cũng đúng. Do đó, \(P \Rightarrow Q\) đúng.
b) Mệnh đề có dạng \(P \Leftrightarrow Q\) với P: “\(a - 2 > b\)” và Q: “\(a > b + 2\)”
Khi P đúng thì Q cũng đúng, do đó, \(P \Rightarrow Q\) đúng.
Khi Q đúng thì P cũng đúng, do đó, \(Q \Rightarrow P\) đúng.
Vậy mệnh đề \(P \Leftrightarrow Q\) đúng.

CM
25 tháng 3 2019
Giả sử phương trình đã cho có 3 nghiệm
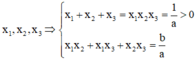
Khi đó
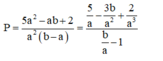
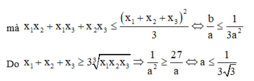
Suy ra
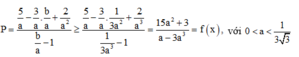
Xét hàm số:
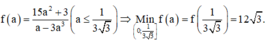
Chọn D.


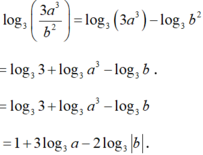

ý tưởng là thế nầy, dấu = thì không biết.
Áp dụng BĐT AM-GM+Bunyakovsky:
\(\left(a+2b\right)\left(ka+kb\right)\le\frac{1}{4}\left[a\left(k+1\right)+b\left(k+2\right)\right]^2\le\frac{1}{4}.\left[\left(k+1\right)^2+\left(k+2\right)^2\right]\left(a^2+b^2\right)\)
\(\le\frac{\left[\left(k+1\right)^2+\left(k+2\right)^2\right]}{4}\left(a+b\right)\)
do đó \(VT\le\frac{\left[\left(k+1\right)^2+\left(k+2\right)^2\right]}{4k}\)
Việc còn lại là tìm k (:v ) Ta thack ngươi tìm đó (:v ) Đùa thôi ,tìm được