Cho tam giác ABC cân tại A; Kẻ AH vuông góc BC
a) CMR: Tam giác ABH= Tam giác ACH
b kẻ HE vuông góc AB; HFvuông góc AC. CMR: tam giác AFE cân
MNG GIÚP T VS Ạ! T CẢM ƠN NHIỀU!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

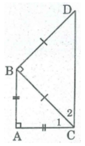
Vì ΔABC vuông cân tại A nên 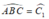
Lại có: 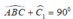 ( tính chất tam giác vuông).
( tính chất tam giác vuông).
Suy ra: ∠ C 1 = 45 0
Vì
∆
BCD vuông cân tại B nên 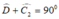
Lại có: ![]() ( tính chất tam giác vuông).
( tính chất tam giác vuông).
Suy ra: ∠ C 2 = 45 0
∠ (ACD) = ∠ C 1 + ∠ C 2 = 45 0 + 45 0 = 90 0
⇒ AC ⊥ CD
Mà AC ⊥ AB (gt)
Suy ra: AB //CD
Vậy tứ giác ABCD là hình thang vuông.

ΔBDC vuông cân tại B
=>góc BCD=góc BDC=45 độ
ΔABC vuông cân tại A
=>góc ABC=góc ACB=45 độ
góc ABC=góc DCB
mà hai góc này ở vị trí so le trong
nên AB//DC
mà AB vuông góc AC
nên DC vuông góc AC
Xét tứ giác ABDC có
AB//DC
góc CAB=90 độ
Do đó: ABDC là hình thang vuông

Vì tam giác ABC vuông cân tại A (gt) nên góc ABC = góc ACB = 90 : 2 = 45 độ
Vì tam giác BCD vuông cân tại B (gt) nên góc BDC = góc BCD = 90 : 2 = 45 độ
Ta có: góc ACB + góc BCD = góc ACD = 45 độ + 45 độ = 90 độ
hay AC vuông góc DC. (1)
Vì tam giác ABC vuông cân tại A (gt) nên AC vuông góc AB (2)
Từ (1) và (2) suy ra DC // AB
Do đó tứ giác ABCD là hình thang.