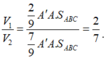Cho lăng trụ ABC.A'B'C', trên cạnh AA'', BB' lấy các điểm M, N sao cho AA' = 3A'M; BB' = 3B'N. Mặt phẳng (C'MN) chia khối lăng trụ đã cho thành hai phần. Gọi là thể tích khối chóp C'.A'B'NM, là thể tích khối đa diện ABC.MNC'. Tính tỉ số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là B
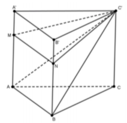
Gọi V là thể tích khối lăng trụ ABC.A'B'C'
![]()
Mà 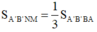
Do đó ![]()
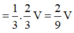
Suy ra 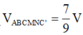
Vậy V 1 V 2 = 2 7

Đáp án C.
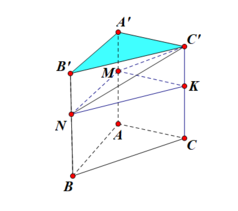
V A B C . M N K = S A B C . C K = 2 3 S A B C . A ' A
V
C
'
M
K
=
1
3
C
'
K
.
S
=
1
9
C
'
C
'
S
A
B
C
=
1
9
A
'
.
A
.
S
A
B
C
⇒
V
2
=
V
A
B
C
.
M
N
K
+
V
C
'
.
M
N
K
=
2
3
S
A
B
C
.
A
A
'
+
1
9
A
'
A
.
S
A
B
C
=
7
9
A
'
A
.
S
A
B
C
V
M
N
K
A
'
B
'
C
'
=
S
M
N
K
.
C
'
K
=
1
3
S
A
B
C
.
A
'
A
⇒ V 1 = V M N K A ' B ' C ' - V C ' M N K = 1 3 S A B C . A ' A - 1 9 A ' A S A B C = 2 9 A ' A S A B C
Vậy : V 1 V 2 = 2 9 A ' A S A B C 7 9 A ' A S A B C = 2 7 .

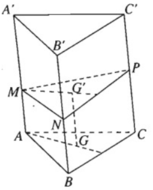
Gọi G và G' lần lượt là trọng tâm của tam giác ABC và tam giác MNP . Ta có:
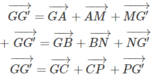
Cộng từng vế với vế ta có:
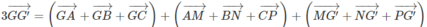
Vì G là trọng tâm của tam giác ABC nên 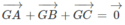
và G' là trọng tâm của tam giác MNP nên:
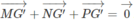
Do đó: 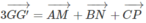
Hay 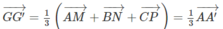
Vì điểm G cố định và 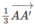 là vectơ không đổi
là vectơ không đổi
nên G' là điểm cố định. Vậy mặt phẳng (MNP) luôn luôn đi qua điểm G' cố định.

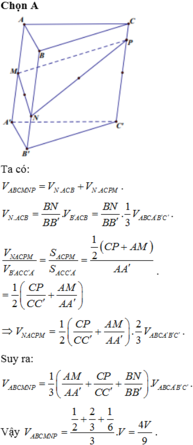
Đáp án là A
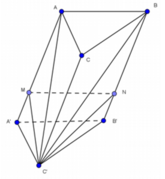
Do AA' = 4A'M, BB' = 4B'N nên suy ra


Mặt khác, ta có
![]()
![]()
Từ (1), (2) 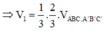
![]()
Vậy 
Từ đó suy ra V 1 V 2 = 1 5
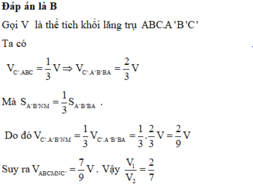


Đáp án C.
Vậy: