1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = (x2 - 2)e2x trên đoạn [-3; 1]
2. Cho hàm số 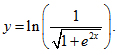 Chứng minh e2y - y' = 1.........
Chứng minh e2y - y' = 1.........
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$
Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$
Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.
Câu 2:
Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$
Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$
Với $x\in (1;3)$ thì hàm luôn nghịch biến
$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$
$\Rightarrow$ hàm không có min, max.

y = x 2 + 2 x + m - 4 = ( x + 1 ) 2 + m - 5
Ta có ( x + 1 ) 2 + m - 5 ∈ m - 5 ; m - 1
Giá trị lớn nhất của hàm số y = x 2 + 2 x + m - 4 trên đoạn[ -2; 1] đạt giá trị nhỏ nhất khi
m - 5 < 0 m - 1 > 0 5 - m = m - 1 ⇔ m = 3
Chọn B.

Đáp án B
Xét hàm số y = x + e 2 x trên đoạn [0;1], ta có y ' = 1 + 2 e 2 x > 0 ∀ x ∈ ( 0 ; 1 ) .
Suy ra hàm số đã cho là hàm số đồng biến trên [0;1].
Khi đó: m a x [ 0 ; 1 ] y = y ( 1 ) = 1 + e 2

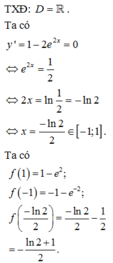
Chọn A.
Chú ý: HS có thể sử dụng chưc năng MODE 7 trên MTCT đẻ giải các bài toán tìm GTLN, GTNN của hàm số trên một đoạn.

Đáp án C.
y ' = 1 − 2 e 2 x
y ' = 0 ⇔ 1 − 2 e 2 x = 0 ⇔ e 2 x = 1 2 ⇔ 2 x = − ln 2 ⇔ x = − ln 2 2 ∈ − 1 ; 1
y − 1 = − 1 − e − 2 ; y 1 = 1 − e 2 ; y − ln 2 2 = − ln 2 2 − 1 2 = − ln 2 + 1 2
Suy ra max − 1 ; 1 y = − ln 2 + 1 2

Ta có y = x 2 + 2 x + a - 4 = x + 1 2 + a - 5
Đặt u = x + 1 2 khi đó ∀ x ∈ - 2 ; 1 thì u ∈ 0 ; 4
Ta được hàm số f u = u + a - 5
Khi đó
M a x x ∈ - 2 ; 1 y = M a x x ∈ 0 ; 4 f u = M a x f 0 , f 4 = M a x a - 5 ; a - 1
Trường hợp 1:
a - 5 ≤ a - 1 ⇔ a ≤ 3 ⇒ M a x x ∈ 0 ; 4 f u = 5 - a ≥ 2 ⇔ a = 3
Trường hợp 2:
a - 5 ≤ a - 1 ⇔ a ≥ 3 ⇒ M a x x ∈ 0 ; 4 f u = a - 1 ≥ 2 ⇔ a = 3
Vậy giá trị nhỏ nhất của M a x x ∈ - 2 ; 1 y = 2 ⇔ a = 3
Đáp án A
1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=(x2−2)e2xy=(x2−2)e2x trên đoạn [−3;1][−3;1]
Để tìm giá trị lớn nhất và nhỏ nhất của hàm số trên một đoạn, ta thực hiện các bước sau:
Ta có: y′=(2x)e2x+(x2−2)(2e2x)=(2x2+2x−4)e2xy′=(2x)e2x+(x2−2)(2e2x)=(2x2+2x−4)e2x
(2x2+2x−4)e2x=0(2x2+2x−4)e2x=0 Vì e2x>0e2x>0 với mọi xx, nên ta chỉ cần giải phương trình 2x2+2x−4=02x2+2x−4=0. Giải phương trình bậc hai này, ta được x=1x=1 hoặc x=−2x=−2.
So sánh các giá trị 7e−67e−6, 2e−42e−4, và −e2−e2. Ta thấy:
2. Cho hàm số y=ln(121+e−−−−√)y=ln(121+e). Chứng minh e2y−y′=1e2y−y′=1
Vì y=ln(121+e−−−−√)y=ln(121+e), ta thấy yy là một hằng số vì không phụ thuộc vào xx. Do đó, y′=0y′=0.
e2y=e2ln(121+e√)=eln((121+e√)2)=eln(1+e4)=1+e4e2y=e2ln(121+e)=eln((121+e)2)=eln(1+e4)=1+e4
Ta có: e2y−y′=1+e4−0=1+e4e2y−y′=1+e4−0=1+e4. Tuy nhiên, đề bài yêu cầu chứng minh e2y−y′=1e2y−y′=1. Có vẻ như có một sự nhầm lẫn trong đề bài hoặc trong cách tính toán.
Nếu đề bài đúng là y=12ln(1+e)y=12ln(1+e), thì: y′=0y′=0 e2y=e2.12ln(1+e)=eln(1+e)=1+ee2y=e2.12ln(1+e)=eln(1+e)=1+e e2y−y′=1+e−0=1+ee2y−y′=1+e−0=1+e
Hoặc nếu đề bài là y=12ln(1+e4)y=12ln(1+e4), thì: y′=0y′=0 e2y=e2.12ln(1+e4)=eln(1+e4)=1+e4e2y=e2.12ln(1+e4)=eln(1+e4)=1+e4 e2y−y′=1+e4−0=1+e4e2y−y′=1+e4−0=1+e4
Như vậy, với đề bài đã cho, không thể chứng minh được e2y−y′=1e2y−y′=1.