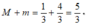Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đặt g ( x ) = 3 f ( x ) - x 3 . Hàm số ban đầu có dạng y=|g(x)|
Ta có g ' ( x ) = 3 f ' ( x ) - 3 x 2 .
Cho g'(x)=0 ⇔ [ x = 0 x = 1 x = 2
Dễ thấy g(0)=0. Ta có bảng biến thiên
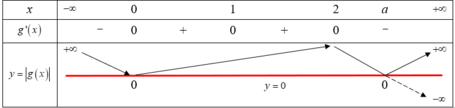
Dựa vào BBT suy ra hàm số y=|g(x)| đồng biến trên khoảng (0;2) và a ; + ∞ với g(a)=0
Chọn đáp án C.
Đáp án D
Định lí: “Nếu hàm số y = f x liên tục trên a ; b và f a . f b < 0 thì tồn tại ít nhất một điểm c ∈ a ; b sao cho f c = 0 ”.
Mệnh đề 1: SAI ở giả thiết (a;b).
Mệnh đề 2: Nếu hàm số y=f(x) liên tục trên a ; b
và f a . f b < 0 thì tồn tại ít nhất một điểm c ∈ a ; b sao cho c hay f x = 0 là nghiệm của phương trình f(x)=0 nên mệnh đề 2 ĐÚNG.
Mệnh đề 3: Nếu hàm số y=f(x) liên tục, đơn điệu trên a ; b và f a . f b < 0 thì đồ thị hàm số y=f(x) cắt trục Ox tại duy nhất một điểm thuộc khoảng (a;b) nên f(x)=0 có nghiệm duy nhất trên (a;b). Do đó mệnh đề 3 ĐÚNG
Đáp án C
Ta có:
9 = ∫ 0 9 f x d x = F x = 0 9 F 9 = F 0 ⇒ F 9 = F 0 + 9 = 12.
thỏa mãn
x
2
f
'
x
+
f
x
=
0
và
f
x
≠
0
,
∀
x
∈
0
;
+
∞
. Tính f(2) biết f(1) = e.
. 
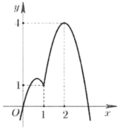
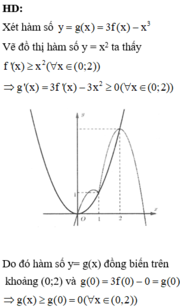
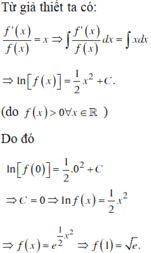
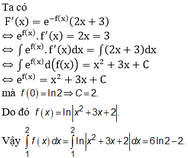
Chọn D
Ta có 3x.f(x) - x 2 f ' ( x ) = 2 f 2 ( x )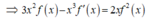
Thay x = 1 vào ta được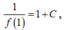
vì f(1) =
1
3
nên suy ra C = 2
Nên
Ta có: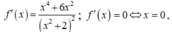 
Khi đó, f(x) đồng biến trên [1;2]
Suy ra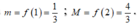
Suy ra