Cho S.ABCD là hình chóp đều. Tính thể tích khối chóp S.ABCD biết
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

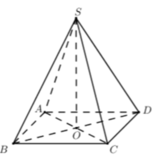
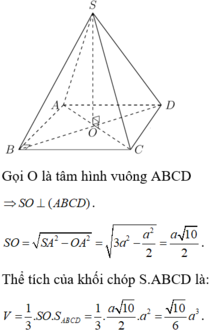
Gọi O = A C ∩ B D ⇒ S O ⊥ A B C D
Tam giác SAC đều cạnh a ⇒ S O = a 3 2 và AC = a ⇒ A B = a 2
Vậy:
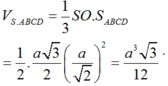
Chọn B.

Đáp án A
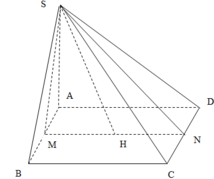
Gọi M, N lần lược là trung điểm của A B , C D ⇒ S M N ⊥ A B C D
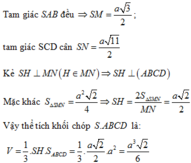

Đáp án A
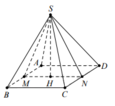
Gọi M, N là trung điểm của A B , C D ⇒ S M N ⊥ A B C D .
Tam giác SAB đều ⇒ S M = a 3 2 ; tam giác SCD cân ⇒ S N = a 11 2 .
Kẻ S H ⊥ M N H ∈ M N ⇒ S H ⊥ A B C D
Mặt khác S ∆ S M N = a 2 2 4 ⇒ S H = 2 . S ∆ S M N M N = a 2 2 .
Vậy thể tích khối chóp S.ABCD là V = 1 3 S H . S A B C D = 1 3 . a 2 2 . a 2 = a 3 2 6 .

Gọi O là tâm hình vuông ABCD,M là trung điểm của SA
Mặt phẳng trung trực của đoạn thẳng SA cắt SO tại I
Điểm I là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD bán kính R=IS
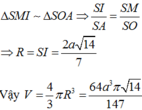
Đáp án C




Chọn C.
Gọi H là hình chiếu của S lên (ABCD)