Cho các tập hợp $A = (-\infty; \, m)$ và $B = [3m+1; \, 3m + 2]$. Tìm $m$ để:
![]() $A \subset C_{\mathbb{R}} B$;
$A \subset C_{\mathbb{R}} B$;
![]() $C_{\mathbb{R}} A \cap B \ne \varnothing$.
$C_{\mathbb{R}} A \cap B \ne \varnothing$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để A hợp B=A thì B là tập con của A
=>2m-5<23 và 23<=-m
=>2m<28 và -m>=23
=>m<=-23 và m<14
=>m<=-23
=>Chọn B

Ta có:
\(E=\left\{x\in R|x< -3\right\}\)
\(\Rightarrow E=\left\{....;-3\right\}\)
\(\Rightarrow E=\left\{-3;-\infty\right\}\)
Vậy chọn C

Tham khảo:
Ta có:

Suy ra phần bù của tập hợp \(\left( { - \infty ; - 2} \right)\) trong \(\mathbb{R}\) là: \(\mathbb{R}{\rm{\backslash }}\left( { - \infty ; - 2} \right) = [ - 2; + \infty )\)

Suy ra phần bù của tập hợp \([ - 5; + \infty )\) trong \(\mathbb{R}\) là: \(\mathbb{R}{\rm{\backslash }}[ - 5; + \infty ) = ( - \infty ; - 5)\)

Giao của hai tập hợp là \([ - 2;3] \cap (1; + \infty ) = (1;3]\)
Hiệu của \(B \backslash A \) là \( (1; + \infty ) \backslash [ - 2;3] = (3; + \infty )\)
Phần bù của B trong \(\mathbb{R}\) là: \({C_\mathbb{R}}\;B = \mathbb{R}{\rm{\backslash }}\;(1; + \infty ) = ( - \infty ;1]\)

Tham khảo:
a) Để xác định tập hợp \(A = ( - \infty ;0] \cup [ - \pi ;\pi ]\), ta vẽ sơ đồ sau đây:
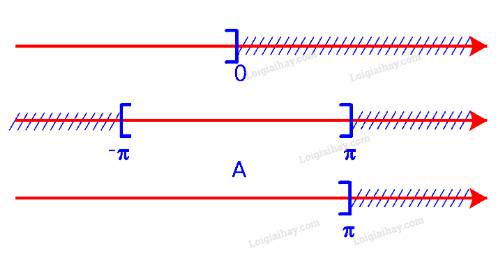
Từ sơ đồ, ta thấy \(A = ( - \infty ;\pi ]\)
b) Để xác định tập hợp \(B = [ - 3,5;2] \cap ( - 2;3,5)\), ta vẽ sơ đồ sau đây:
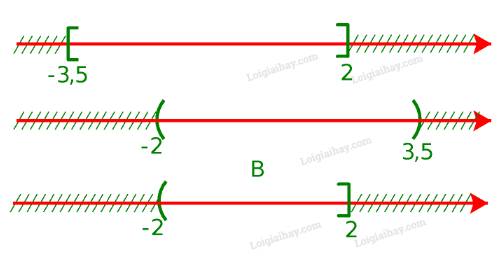
Từ sơ đồ, ta thấy \(B = ( - 2;2]\)
c) Để xác định tập hợp \(C = ( - \infty ;\sqrt 2 ] \cap [1; + \infty )\), ta vẽ sơ đồ sau đây:
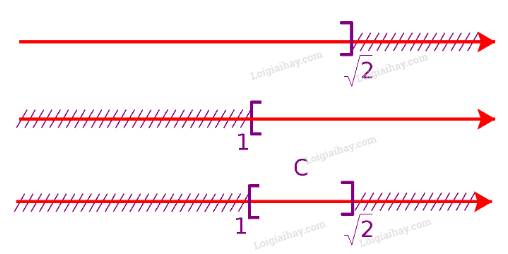
Từ sơ đồ, ta thấy \(C = [1;\sqrt 2 ]\)
d) Để xác định tập hợp \(D = ( - \infty ;\sqrt 2 ]{\rm{\backslash }}[1; + \infty )\), ta vẽ sơ đồ sau đây:
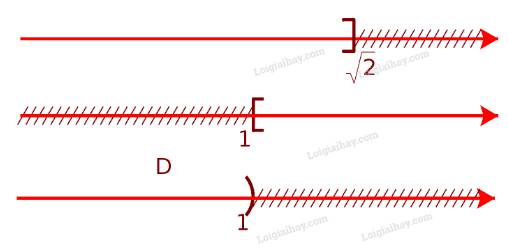
Từ sơ đồ, ta thấy \(D = ( - \infty ;1)\)

Tham khảo:
a) Để xác định tập hợp \(A = (1;3) \cup [ - 2;2]\), ta vẽ sơ đồ sau đây:
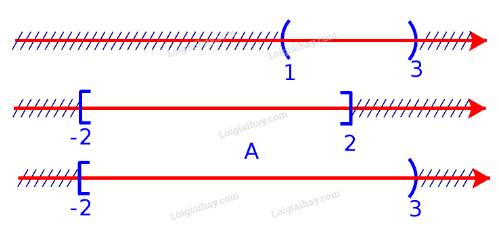
Từ sơ đồ, ta thấy \(A = [ - 2;3)\)
b) Để xác định tập hợp \(B = ( - \infty ;1) \cap [0;\pi ]\), ta vẽ sơ đồ sau đây:
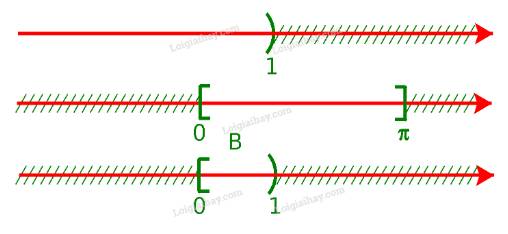
Từ sơ đồ, ta thấy \(B = [0;1)\)
c) Để xác định tập hợp \(C = [\frac{1}{2};3){\rm{\backslash }}(1; + \infty )\), ta vẽ sơ đồ sau đây:
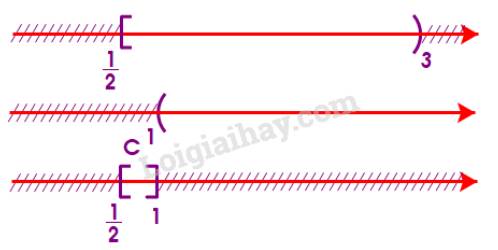
Từ sơ đồ, ta thấy \(C = [\frac{1}{2};1]\)
d) Để xác định tập hợp \(D = {C_\mathbb{R}}[ - 1; + \infty )\), ta vẽ sơ đồ sau đây:
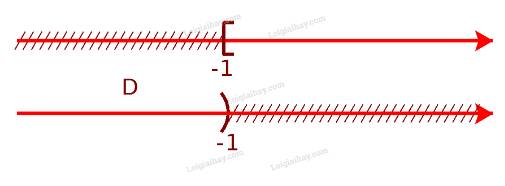
Từ sơ đồ, ta thấy \(D = ( - \infty ; - 1)\)
✳️ Giải thích các điều kiện
📌 Điều kiện 1: \(A \subset \mathbb{R} \backslash B\)
👉 Điều này xảy ra khi:
\(\left(\right. - \infty ; m \left.\right) \cap \left[\right. 3 m + 1 ; 3 m + 2 \left]\right. = \emptyset\)
→ Tức là:
\(m \leq 3 m + 1\)
Giải bất phương trình:
\(m \leq 3 m + 1 \Rightarrow - 2 m \leq 1 \Rightarrow m \geq - \frac{1}{2}\)
📌 Điều kiện 2: \(A \cap B \neq \emptyset\)
Tức là: phải có phần tử chung giữa \(A = \left(\right. - \infty ; m \left.\right)\) và \(B = \left[\right. 3 m + 1 ; 3 m + 2 \left]\right.\)
→ Tức là:
\(\left(\right. - \infty ; m \left.\right) \cap \left[\right. 3 m + 1 ; 3 m + 2 \left]\right. \neq \emptyset\)
→ Điều này xảy ra khi tồn tại \(x \in \left[\right. 3 m + 1 ; 3 m + 2 \left]\right.\) sao cho \(x < m\)
→ Nói cách khác:
\(3 m + 1 < m\)
Giải bất phương trình:
\(3 m + 1 < m \Rightarrow 2 m < - 1 \Rightarrow m < - \frac{1}{2}\)
✅ Kết luận
⛔ Hai điều kiện mâu thuẫn nhau → Không có giá trị \(m\) nào thỏa mãn đồng thời cả hai điều kiện.
1và 1/12 bằng bao nhiêu