Bài 3: Cho (d1): y = -2x ; (d2): y = x – 3 ; (d3): y = mx + 4 a) Tìm tọa độ giao điểm của hai đường thẳng d1 và d2 b) Tìm các giá trị tham số m để 3 đường thẳng d1, d2, d3 đồng quy.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 12 2021
PT hoành độ giao điểm \(\left(d_1\right)\) và \(\left(d_2\right)\)
\(2x+1=3x-1\Leftrightarrow x=2\Leftrightarrow y=5\Leftrightarrow A\left(2;5\right)\)
Thay \(x=2;y=5\) vào \(\left(d_3\right)\Leftrightarrow2+3=5\) (đúng)
Do đó \(A\left(2;5\right)\in\left(d_3\right)\)
Vậy \(\left(d_1\right);\left(d_2\right);\left(d_3\right)\) đồng quy tại \(A\left(2;5\right)\)
10 tháng 12 2021
\(\left\{{}\begin{matrix}2x+1=3x-1\\y=2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=5\end{matrix}\right.\)
Thay x=2 và y=5 vào y=x+3, ta được:
2+3=5(đúng)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2021
Do giao điểm có tung độ bằng 3 nên hoành độ thỏa mãn:
\(3=-2x+1\Rightarrow x=-1\)
Thế tọa độ giao điểm vào pt d2 ta được:
\(3=-\left(2m-3\right)+3-m\)
\(\Rightarrow-3m+3=0\Rightarrow m=1\)
8 tháng 10 2019
BÀI 1
để d1 và d2 // thì: m-3=-1(1) ; m khác 3 (2)
ta có: (1) <=> m=2 (3)
từ (2) và (3) => để d1//d2 thì m = 2
8 tháng 9 2021
Bài 3:
Vì (d)//(d1) nên a=3
Vậy: (d): y=3x+b
Thay \(x=\dfrac{2}{3}\) và y=0 vào (d), ta được:
\(b+2=0\)
hay b=-2
2 tháng 6 2017
bài này dễ mà bạn :
\(d_1,d_2\)cắt nhau tại diểm có tung độ là 3 nên hoành độ của giao điểm là :
(thay \(y=3\)vào \(d_1\)) \(3=-2x+1\Leftrightarrow-2x=2\Leftrightarrow x=-1\)Tọa độ của giao điểm cũng thỏa mãn phương trình \(d_2\)nên: \(3=-\left(2m-3\right)+3-m\Leftrightarrow-3m=-3\)\(\Leftrightarrow m=1\)
9 tháng 8 2023
2:
a: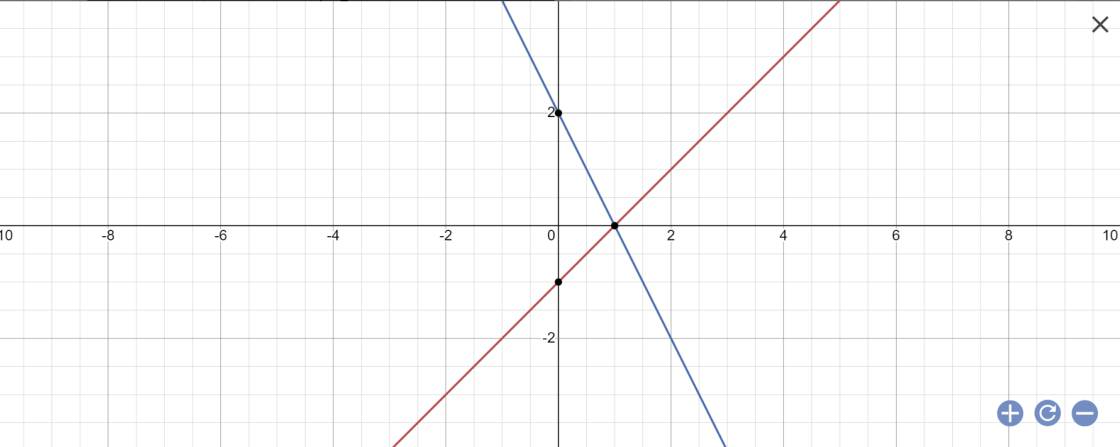 
b: Tọa độ giao điểm là nghiệm của hệ:
x-1=-2x+2 và y=x-1
=>3x=3 và y=x-1
=>x=1 và y=1-1=0
1:
a: Thay x=-1 và y=0 vào (d), ta được:
m+1=0
=>m=-1
c: tọa độ giao điểm là:
2x-2=-x+4 và y=2x-2
=>3x=6 và y=2x-2
=>x=2 và y=4-2=2
Thay x=2 và y=2 vào (d), ta được:
m-2=2
=>m=4
12 tháng 1 2023
Khi m=3 thì (d): y=2x+3
Lấy A(0;3) thuộc (d)
(d1): y=2x-3
=>2x-y-3=0
\(h\left(A;d1\right)=\dfrac{\left|0\cdot2+\left(-1\right)\cdot3+\left(-3\right)\right|}{\sqrt{2^2+1^2}}=\dfrac{6}{\sqrt{5}}\)
25 tháng 1 2024
a: Tọa độ A là:
\(\left\{{}\begin{matrix}x+2=-x-2\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=-4\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-2+2=0\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x+2=-2x+2\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=0\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0+2=2\end{matrix}\right.\)
Tọa độ C là:
\(\left\{{}\begin{matrix}-x-2=-2x+2\\y=-x-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=4\\y=-4-2=-6\end{matrix}\right.\)
Vậy: A(-2;0); B(0;2); C(4;-6)
b: \(AB=\sqrt{\left(0+2\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)
\(AC=\sqrt{\left(4+2\right)^2+\left(-6-0\right)^2}=6\sqrt{2}\)
\(BC=\sqrt{\left(4-0\right)^2+\left(-6-2\right)^2}=\sqrt{4^2+8^2}=4\sqrt{5}\)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=0\)
=>\(\widehat{BAC}=90^0\)
=>ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\sqrt{2}\cdot6\sqrt{2}=12\)
a. PTTDGD của (d1) và (d2):
\(-2x=x-3\)
\(\Rightarrow x=1\)
Thay x = 1 vào (d1): \(y=-2\cdot1=-2\)
Vậy (d1) cắt (d2) tại điểm A(1;-2)
Lời giải:
a. PT hoành độ giao điểm: $-2x=x-3$
$\Leftrightarrow x=1$
$y=-2x=1(-2)=-2$
Vậy giao điểm của $(d_1), (d_2)$ là $(1,-2)$
b.
Để $(d_1), (d_2), (d_3)$ đồng quy thì $(d_3)$ cũng đi qua giao điểm của $(d_1), (d_2)$
Tức là $(1,-2)\in (d_3)$
$\Leftrightarrow -2=m.1+4\Leftrightarrow m=-6$