Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

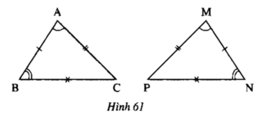
Hai tam giác bằng nhau vì có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau
kí hiệu: ΔABC = ΔMNP

Trước hết ta xác định B và K là hai đỉnh tương ứng. Sau đó từ AB = KD suy ra A vad D là hai đỉnh tương ứng. Vậy \(\Delta ABC=\Delta DKH\)
Ta có: ∠B = ∠K nên đỉnh B tương ứng với đỉnh K
AB = KD nên đỉnh D tương ứng với đỉnh A
= > đỉnh C tương ứng với đỉnh H
Vậy ∆ABC = ∆ DKH

a: ΔABC và ΔEFD
Để ΔABC=ΔEFD theo trường hợp c-g-c thì BC=FD
b: ΔABC=ΔEFD
nên AB=EF=5cm; AC=ED=6cm; BC=FD=6cm
=>\(C_{ABC}=C_{EFD}=5+6+6=17\left(cm\right)\)

1:
ΔDEF=ΔMNP
=>DE=MN; EF=NP; DF=MP
EF+FD=10; NP-MP=2; DE=3
=>MN=3cm; EF-DF=2 và EF+FD=10
=>EF=(10+2)/2=6cm và DF=6-2=4cm
EF=NP=6cm; DF=MP=4cm
2:
a: ΔABC=ΔNMP
b: ΔABC=ΔPNM
Bài 1
Do ∆DEF = ∆MNP
⇒ DE = MN; DF = MP; EF = NP
Do NP - MP = 2 (cm)
⇒ EF - FD = 2 (cm)
Lại có
EF + FD = 10 (cm)
⇒ EF = (10 + 2) : 2 = 6 (cm)
⇒ FD = 10 - 6 = 4 (cm)
Vậy độ dài các cạnh của mỗi tam giác là:
EF = NP = 6 cm
FD = MP = 4 cm
DE = MN = 3 cm
💡 Đề bài
Cho hình vẽ dưới đây, tam giác \(\triangle D E F\) và \(\triangle A B C\) có bằng nhau không? Vì sao?
👉 Nếu có, hãy viết ký hiệu bằng nhau.
📐 Giải nhanh siêu dễ hiểu:
✨ Giả sử đề bài cho:
📘 Ta dùng:
Trường hợp bằng nhau cạnh - góc xen giữa - cạnh (c.g.c)
💬 Nếu 2 tam giác có 2 cạnh bằng nhau và góc xen giữa bằng nhau ⇒ 2 tam giác bằng nhau.
✅ Vậy nếu:
⟹ \(\triangle A B C = \triangle D E F\) (theo c.g.c)
📝 Ký hiệu bằng nhau
📌 \(\triangle A B C = \triangle D E F\) (c.g.c) Chúc bạn học tốt nho !