Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,Diện tích hình chữ nhật ABCD là:(20:2-6)x6=24(cm)
b,Đường chéo hình thoi là:
HF=AB=6cm
EG=BC=4cm
Diện tích hình thoi là:(6x4):2=12(cm^2)

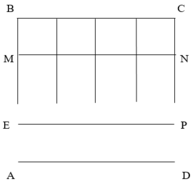
Trước hết Ta xét các hình chữ nhật tạo bởi hai đoạn AD, EP và các đoạn nối các điểm trên hai cạnh AD và BC. Bằng cách tương tự như tronh ví dụ 1 ta tính được 10 hình.
Tương tự ta tính được số hình chữ nhật tạo thành do hai đoạn EP và MN, do MN và BC đều bằng 10.
Tiếp theo ta tính số hình chữ nhật tạo thành do hai đoạn AD và MN, EP và BC với các đoạn nối các điểm trên hai cạnh AD và BC đều bằng 10.
Vì vậy :
Số hình chữ nhật đếm được trên hình vẽ là :
10 + 10 + 10 + 10 + 10 + 10 = 60 (hình)
Đáp số 60 hình.

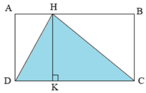
Kẻ HK vuông góc với CD, khi đó HK là chiều cao tương ứng với cạnh đáy CD.
Ta có chiều cao HK bằng chiều rộng của hình chữ nhật ABCD hay HK = BC = 24cm
Vì ABCD là hình chữ nhật nên CD = AB = 37cm.
Diện tích tam giác HDC là:
37 × 24 : 2 = 444( c m 2 )
Đáp số: 444 c m 2
Đáp án A


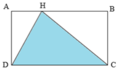
Ta có: * \(\frac{S_{\Delta ADE}}{S_{\Delta ADB}}=\frac{1}{2}\) mà \(\frac{S_{\Delta ADB}}{S_{ABCD}}=\frac{1}{2}\) suy ra \(\frac{S_{\Delta ADE}}{S_{ABCD}}=\frac{1}{4}\)
* \(\frac{S_{\Delta DCM}}{S_{\Delta DCB}}=\frac{1}{2}\) mà \(\frac{S_{\Delta CDB}}{S_{ABCD}}=\frac{1}{2}\) suy ra \(\frac{S_{\Delta DCM}}{S_{ABCD}}=\frac{1}{4}\)
* \(\frac{S_{\Delta EBM}}{S_{\Delta EBC}}=\frac{1}{2}\) mà \(\frac{S_{\Delta EBC}}{S_{\Delta ABC}}=\frac{1}{2}\) suy ra \(\frac{S_{\Delta EBM}}{S_{\Delta ABC}}=\frac{1}{4}\)
tuy nhiên \(\frac{S_{\Delta EBC}}{S_{ABCD}}=\frac{1}{4}\) suy ra \(\frac{S_{\Delta EBM}}{S_{ABCM}}=\frac{1}{8}\)
Ta lại có: \(\frac{S_{\Delta DEM}}{S_{ABCD}}=S_{ABCD}-\left(S_{\Delta ADE}+S_{\Delta EBM}+S_{\Delta DCM}\right)=1-\left(\frac{1}{4}+\frac{1}{4}+\frac{1}{8}\right)=\frac{3}{8}\)
\(\Rightarrow\) \(S_{ABCD}=S_{\Delta DEM}\div\frac{3}{8}=6\times\frac{8}{3}=16\left(cm^2\right)\)
hình vẽ đâu bạn 🤔🤔🤔