LG
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
13 tháng 9 2020
Chú ý: Từ tháng 5/2017, cứ vào Thứ Bảy hàng tuần, Online Math sẽ có 03 giải thưởng là thẻ cào điện thoại 50.000đ cho các bạn có điểm hỏi đáp cao nhất trong tuần và 03 giải thưởng là 2 tháng VIP cho các bạn có điểm số hỏi đáp cao tiếp theo trong tuần. Khi một bạn đã được thưởng VIP, bạn ấy sẽ không được thưởng trong 4 tuần sau đó cho dù điểm số hỏi đáp nằm trong top 5 và các bạn có điểm cao tiếp theo sẽ có cơ hội nhận thưởng.
8 tháng 8 2018
\(\left|x\right|=2\Rightarrow\orbr{\begin{cases}x=2\\x=-2\end{cases}}\)
Khi x = 2 thì \(5x^2-2x+3x-1=5.2^2-2.2+3.2-1=20-4+6-1=21\)
Khi x = -2 thì \(5x^2-2x+3x-1=5.\left(-2\right)^2-2.\left(-2\right)+3.\left(-2\right)-1\)
\(=20+4-6-1=17\)
DD
Đoàn Đức Hà
Giáo viên
2 tháng 6 2021
\(\overline{14a3}+\overline{35b2}=1403+10a+3502+10b=4905+9\left(a+b\right)+\left(a+b\right)⋮9\)
\(\Leftrightarrow a+b⋮9\).
Do đó ta có các trường hợp sau:
- \(\hept{\begin{cases}a+b=0\\a-b=3\end{cases}}\Leftrightarrow\hept{\begin{cases}a=\frac{3}{2}\\b=-\frac{3}{2}\end{cases}}\left(l\right)\)
- \(\hept{\begin{cases}a+b=9\\a-b=3\end{cases}}\Leftrightarrow\hept{\begin{cases}a=6\\b=3\end{cases}}\left(tm\right)\)
- \(\hept{\begin{cases}a+b=18\\a-b=3\end{cases}}\Leftrightarrow\hept{\begin{cases}a=\frac{21}{2}\\b=\frac{15}{2}\end{cases}}\left(l\right)\)
Vậy \(a=6,b=3\).
XO
2 tháng 6 2021
Ta có 14a3 + 35b2
= 1000 + 400 + 10a + 3 + 3000 + 500 + 10b + 2
= 4905 + 10(a + b)
mà 14a3 + 35b2 \(⋮\)9
lại có 4905 \(⋮\)9
=> 10(a + b) \(⋮\)9
=> a + b \(⋮\)9 (vì 10 không chia hết cho 9)
Vì \(0\le a;b\le9\)
mà a - b = 3
=> Các cặp (a;b) tìm được là (9 ; 6) ; (8;5) ; (7;4) ; (6;3) ; (5;2) (4;1) ; (3;0) (1)
mà a + b \(⋮\)9 (2)
Từ (1);(2) => cặp (a;b) tìm được là (6;3)
Vậy a = 6;b = 3
XO
3 tháng 8 2021
Với n = 0 thì \(\sqrt{1^3+2^3+3^3+..+n^3}=1+2+3+...+n\)(1)
Với n = 1 thì (1) đúng
Giả sử với n = k thì (1) đúng
Ta chứng minh với n = k + 1 thì (1) đúng
Tức là chứng minh khi \(\sqrt{1^3+2^3+3^3+...+k^3}=1+2+3+...+k\)
thì \(\sqrt{1^3+2^3+...+\left(k+1\right)^3}=1+2+3+...+k+1\)(2)
Từ (2) \(\Rightarrow1^3+2^3+3^3+...+\left(k+1\right)^3=\left(1+2+3+...+k\right)^2\)
Khi đó (1 + 2 + 3 + ... + k + 1)2 = [(k + 1)(k + 2) : 2]2 = \(\frac{\left[\left(k+1\right)\left(k+2\right)\right]^2}{4}\)(3)
Lại có \(1^3+2^3+3^3+...+k^3+\left(k+1\right)^3=\left(1+2+3+...+k\right)^2+\left(k+1\right)^3\)
\(=\frac{k^2\left(k+1\right)^2}{4}+\left(k+1\right)^3=\left(k+1\right)^2\left[\frac{k^2}{4}+k+1\right]\)
\(=\frac{\left(k+1\right)^2\left(k^2+4k+4\right)}{4}=\frac{\left(k+1\right)^2\left(k+2\right)^2}{4}=\frac{\left[\left(k+1\right)\left(k+2\right)\right]^2}{4}\)(4)
Từ (3) (4) \(\Rightarrow1^3+2^3+3^3+...+\left(k+1\right)^3=\left(1+2+3+...+k\right)^2\)
\(\Rightarrow\left(2\right)\text{đúng}\Rightarrow\text{đpcm}\)
NM
Nguyễn Minh Quang
Giáo viên
3 tháng 8 2021
đầu tiên ta có :
\(1+2+3+..+n=\frac{n\left(n+1\right)}{2}\) ( cái này thì dễ rồi ha)
ta sẽ chứng minh : \(1^3+2^3+..+n^3=\left[\frac{n\left(n+1\right)}{2}\right]^2\) bằng quy nạp
đẳng thức đúng với n =1
giả sử đẳng thức đúng với n=k , tức là :
\(1^3+2^3+..+k^3=\left[\frac{k\left(k+1\right)}{2}\right]^2\)
ta sẽ chứng minh đúng với n=k+1, thật vậy
ta có : \(1^3+2^3+..+k^3+\left(k+1\right)^3=\left[\frac{k\left(k+1\right)}{2}\right]^2+\left(k+1\right)^3=\left(k+1\right)^2\left[\frac{k^2}{4}+k+1\right]=\frac{\left(k+1\right)^2\left(k+2\right)^2}{4}\)
Vậy đẳng thức đúng với k+1, theo nguyên lý quy nạp ta có điều phải chứng minh
31 tháng 8 2017
\(\frac{1}{6}:\frac{-5}{11}=\frac{-11}{30}\)
\(\frac{-11}{30}=-0,3\left(6\right)\)
\(\frac{4}{9}:\frac{-7}{18}=\frac{-8}{7}\)
\(\frac{-8}{7}=-1\left(142857\right)\)
17 tháng 6 2020
Giải:
+) Cứ mỗi bước xóa 2 số thêm 1 số nghĩa là sẽ mất đi một số. Thực hiện 2019 lần theo quy tắc trên thì sẽ còn lại duy nhất 1 số
+) Dễ thấy trong 2020 phân số trên có số 1010/2020 = 1/2
+) Khi các em xóa đến một số bất kì x khác 1/2 thuộc dãy 2020 phân số đó và số 1/2 thì số mới xuất hiện sẽ là: 1/2 + x - 2.1/2 .x = 1/2
Như vậy các e xóa đủ 2019 lần thì vẫn chỉ còn số 1/2
WH
6 tháng 7
Ta gọi phép thay thế hai số \(a , b\) thành \(a + b - 2 a b\) là một phép toán \(\star\). Xét biểu thức:
\(a \star b = a + b - 2 a b\)
Ta biến đổi:
\(1 - \left(\right. a \star b \left.\right) = 1 - a - b + 2 a b = \left(\right. 1 - a \left.\right) \left(\right. 1 - b \left.\right)\)
Đặt \(A = 1 - x\), ta thấy rằng khi thực hiện phép toán, giá trị \(A\) mới bằng tích của hai giá trị \(A\) cũ. Do đó, tích các giá trị \(A = 1 - x\) là một đại lượng bất biến trong toàn bộ quá trình.
Ban đầu, dãy số gồm:
\(\frac{1}{2020} , \frac{2}{2020} , \ldots , \frac{2020}{2020}\)
Tương ứng, các giá trị bất biến là:
\(1 - \frac{1}{2020} , \&\text{nbsp}; 1 - \frac{2}{2020} , \&\text{nbsp}; \ldots , \&\text{nbsp}; 1 - \frac{2020}{2020} = \frac{2019}{2020} , \&\text{nbsp}; \frac{2018}{2020} , \&\text{nbsp}; \ldots , \&\text{nbsp}; 0\)
Vì có một giá trị bằng 0, nên tích các giá trị bất biến ban đầu bằng 0. Do tích này không đổi, nên sau 2019 lần biến đổi, chỉ còn lại một số duy nhất \(x\), thỏa mãn:
\(1 - x = 0 \Rightarrow x = 1\)
Kết luận: Số còn lại trên bảng là \(\boxed{1}\).
13 tháng 10 2021
a) \(\Rightarrow\left(x-3\right)\left(x+4\right)=5.12\)
\(\Rightarrow x^2+x-72=0\)
\(\Rightarrow\left(x-8\right)\left(x+9\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=8\\x=-9\end{matrix}\right.\)
b) \(\Rightarrow\left(x+3\right)^2=36\)
\(\Rightarrow\left[{}\begin{matrix}x+3=6\\x+3=-6\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-9\end{matrix}\right.\)
c) \(\Rightarrow2x^2=8\Rightarrow x^2=4\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
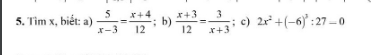
chắc đang chục chặc gì đó hoặc bị lỗi đó bạn .
Chắc tuần này thầy cô bận chưa reset thôi bạn