Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét tứ giác CDME có
^MEC = ^MDC = 900
mà 2 góc này kề, cùng nhìn cạnh MC
Vậy tứ giác CDME là tứ giác nt 1 đường tròn
b, bạn ktra lại đề

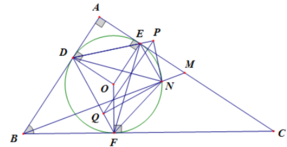
Vì DPN+DQN=90o+90o=180o nên DPNQ là tứ giác nội tiếp
=>QPN=QDN (hai góc nội tiếp cùng chắn cung QN) (5)
Mặt khác DENF là tứ giác nội tiếp nên QDN=FEN (6)
Từ (5) và (6) ta có FEN=QPN (7)
Tương tự ta có: EFN=PQN (8)
Từ (7) và (8) suy ra Δ N P Q ~ Δ N E F ( g . g ) = > P Q E F = N Q N F
Theo quan hệ đường vuông góc – đường xiên, ta có
N Q ≤ N F = > P Q E F = N Q N F ≤ 1 = > P Q ≤ E F
Dấu bằng xảy ra khi Q ≡ F ⇔ NF ⊥ DF ⇔ D, O, N thẳng hàng.
Do đó PQ max khi M là giao điểm của AC và BN, với N là điểm đối xứng với D qua O.

A B C H M N
a, Vì HM là đường cao => \(HM\perp AB\)=> ^HMA = 900
Vì HN là đường cao => \(HN\perp AC\)=> ^HNA = 900
Xét tứ giác AMHN có :
^HMA + ^HNA = 900
mà ^HMA ; ^HNA đối nhau
Vậy tứ giác AMHN nội tiếp
b, Xét tam giác ABH vuông tại H, đường cao HM ta có :
\(AH^2=AM.AB\)(1)
Xét tam giác ACH vuông tại H, đường cao HN ta có :
\(AH^2=AN.AC\)(2)
từ (1) ; (2) suy ra : \(AM.AB=AN.AC\Rightarrow\frac{AM}{AC}=\frac{AN}{AB}\)
Xét tam giác AMN và tam giác ACB ta có :
^A chung
\(\frac{AM}{AC}=\frac{AN}{AB}\)( cmt )
Vậy tam giác AMN ~ tam giác ACB ( c.g.c )
Xét đường tròn (O), ta thấy \(\hat{BAM}=\hat{CAM}\) và 2 góc này lần lượt là 2 góc nội tiếp chắn cung BM và CM nên \(\overgroup{BM}=\overgroup{CM}\) không chứa A của (O). Mà P thuộc (O) nên \(\hat{BPM}=\hat{CPM}\) , suy ra PM là tia phân giác của góc \(\hat{BPC}\). (1)
Mặt khác, vẽ đường tròn (I) nội tiếp tam giác ABC thì đường tròn này tiếp xúc với BC, CA, AB lần lượt tại chính các điểm D, E, F. Xét đường tròn (I), có 2 tiếp tuyến tại D và E cắt nhau tại C nên \(CD=CE\). Tương tự, ta có \(BD=BF\), suy ra \(\frac{DB}{DC}=\frac{BF}{CE}\) (2)
Trong đường tròn (AFE) có \(\hat{AFP}=\hat{AEP}\) (vì cùng là góc nội tiếp chắn cung AP). Từ đó suy ra \(\hat{PFB}=\hat{PEC}\) (vì lần lượt cùng bù với 2 góc trên) (3). Trong đường tròn (O), có \(\hat{PBA}=\hat{PCA}\) (vì cùng là góc nội tiếp chắn cung AP) hay \(\hat{PBF}=\hat{PCE}\) (4).
Từ (3) và (4), suy ra tam giác PFB và PEC đồng dạng, suy ra \(\frac{BF}{CE}=\frac{PB}{PC}\) (5)
Từ (2) và (5), suy ra \(\frac{DB}{DC}=\frac{PB}{PC}\left(=\frac{BF}{CE}\right)\). Theo định lý đường phân giác trong tam giác, suy ra PD là tia phân giác của \(\hat{BPC}\). (6)
Từ (1) và (6), suy ra P, D, M thẳng hàng (vì cùng nằm trên đường phân giác của \(\hat{BPC}\)). Ta có đpcm.
Nếu bạn không xem được hình thì bạn vào trang cá nhân của mình xem nhé.