Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

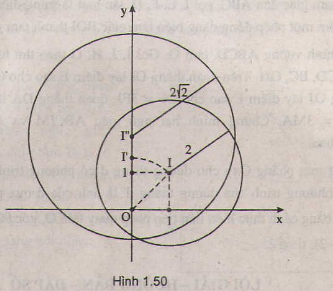
Phép quay tâm O, góc , biến I thành I'(0;
), phép vị tự tâm O, tỉ số
biến I' thành I'' = (0;
.
) = (0;2). Từ đó suy ra phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc
và phép vị tự tâm O, tỉ số
biến đường tròn (I;2) thành đường tròn (I'';2
). Phương trình của đường tròn đó là
+
= 8
Phép quay tâm O, góc , biến I thành I'(0;
), phép vị tự tâm O, tỉ số
biến I' thành I'' = (0;
.
) = (0;2). Từ đó suy ra phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc
và phép vị tự tâm O, tỉ số
biến đường tròn (I;2) thành đường tròn (I'';2
). Phương trình của đường tròn đó là
+
= 8

Gọi I' là ảnh của I qua phép biến hình nói trên
a) Phương trình của đường tròn (I;3) là ( +
= 9
b) (I) = I' (1;-1), phương trình đường tròn ảnh :
c) (I) = I'(3;2), phương trình đường tròn ảnh:
d) (I) = I'( -3;2), phương trình đường tròn ảnh:
Gọi I' là ảnh của I qua phép biến hình nói trên
a) Phương trình của đường tròn (I;3) là ( +
= 9
b) (I) = I' (1;-1), phương trình đường tròn ảnh :
c) (I) = I'(3;2), phương trình đường tròn ảnh:
d) (I) = I'( -3;2), phương trình đường tròn ảnh:

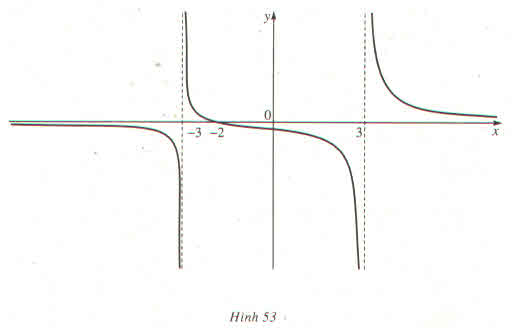
Quan sát đồ thị ta thấy x → -∞ thì f(x) → 0; khi x → 3- thì f(x) → -∞;
khi x → -3+ thì f(x) x → +∞.
b) f(x) =
=
= 0.
f(x) =
=
= -∞ vì
=
> 0 và
= -∞.
f(x) =
=
.
= +∞
vì
=
=
> 0 và
= +∞.

a) Giả sử ta có hai đường xiên SA, SB và các hình chiếu HA, HB của chúng trên mp(α)
Giả sử HA = HB
Vì SH ⊥ mp(α) nên SH ⊥ HA và SH ⊥ SB và các tam giác SHA, SHB là các tam giác vuông. Hai tam giác vuông SHA, SHB có canh SH chung và HA = HB nên :
ΔSHA = ΔSHB SA = SB
Ngược lại nếu SA = SB thì ΔSHA = ΔSHB ⇒ HA = HB
Kết quả, ta có HA = HB SA= SB (đpcm)
b) Giả sử có hai đường xiên SA, SC và các hình chiếu HA, HC của chúng trên mp(α) với giả thiết HC > HA.
Trên đoạn HC, lấy điểm B' sao cho HA' = HA ⇒ HC > HA'. Như vậy, theo kết quả câu a) ta có SA' = SA. Ta có trong các tam giác vuông SHB', SHC thì :
SC2= SH2 + HC2
SA2 = SH2 + HA2
Vì HC > HA' nên SC2 > SA2 ⇒ SC > SA
Suy ra SC > SA
Như vậy HC > HA ⇒ SC > SA
Lí luận tương tự, ta có : SC > SA ⇒ HC > HA
Kết quả : HC > HA ⇔ SC > SA
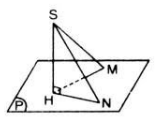
a) Gọi SN là một đường xiên khác. Xét hai tam giác vuông SHM và SHN có SH chung. Nếu SM = SN => tam giác SHM = tam giác SHN => HM = HN, ngược lại nếu HM = HN thì tam giác SHM = tam giác SHNSM => SM = SN.
b) Xét tam giác vuông SHM và SHN có SH chung. Nếu SN > SM thì \(HN^2-SN^2-SH^2\) => \(SM^2-SH^2=HM^2\) => HN > HM. Chứng minh tương tự cho chiều ngược lại.


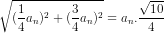 với n ε N*.
với n ε N*. 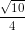




📐 Kết quả chuẩn toán học:
Đây là bài toán nổi tiếng trong hình học:
\(a = R \cdot \frac{\sqrt{3}}{2}\)
Với \(R = 1\) km:
\(a = \frac{\sqrt{3}}{2} \approx \frac{1.732}{2} = 0.866 \&\text{nbsp};\text{km}\)
✅ Kết luận:
Giá trị nhỏ nhất của \(a\) là:
\(\boxed{a = \frac{\sqrt{3}}{2} \approx 0.866 \&\text{nbsp};\text{km}}\)