Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Sử sụng hệ thức: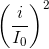 
+
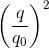= 1
Thay số và giải hệ phương trình trìm I0 và q0
Tần số góc: ω =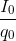 
= 50 (rad/s)
Do mạch chỉ có L nên u và i luôn vuông pha nhau.
Phương trình của i có dạng: (1)
và Phương trình của i có dạng: (2)
Từ (1) và (2) suy ra
Ta có hệ :
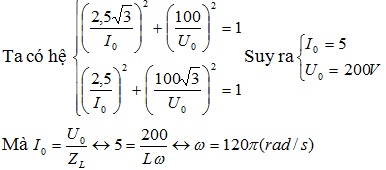
Ta có : \(\frac{T_{W_{\text{đ}}}}{6}=1,5.10^{-4}\)
\(\Rightarrow\frac{T_q}{6}=\frac{2T_{W_{\text{đ}}}}{6}=3.10^{-4}\)
Vậy chọn D.
\(W_t=W_0-W_d=W_0-W_0sin^2\left(\omega t\right)=W_0cos^2\left(\omega t\right)\\\)
\(\Rightarrow W_{tmax}\Leftrightarrow cos^2\left(\omega t\right)=1\\ \Rightarrow W_{tmax}=W_0\)
Ta có: \(\left(\frac{v}{x}\right)'=\frac{v^2-ax}{v^2}\)
Mà: \(a=-\omega^2x\) nên \(\left(\frac{v}{x}\right)'=1+\frac{\omega^2x}{v^2}=1+\frac{x^2}{\frac{v^2}{\omega^2}}=1+\frac{x^2}{A^2-x^2}\)
Đạo hàm 2 vế biểu thức đã cho ta có:
\(1+\frac{x_1^2}{A^2-x_1^2}+1+\frac{x_2^2}{A^2-x_2^2}=1+\frac{x_3^2}{A^2-x_3^2}\)
Thay số vào ta tìm đc giá trị \(x_0\)
Gia tốc cực đại: \(a_{max}=\omega^2.A=(2\pi.2,5)^2.0,05=12,3m/s^2\)
Để làm câu hỏi này, ta áp dụng 2 kết quả sau: Với mạch RLC có \(\omega\)thay đổi:
+ Khi \(U_{Lmax}\) thì \(\omega_0=\frac{1}{C\sqrt{\frac{L}{C}-\frac{R^2}{2}}}\)(1)
+ Khi \(\omega=\omega_1\) hoặc \(\omega=\omega_2\) thì điện áp 2 đầu cuộn dây có cùng giá trị và khi \(\omega=\omega_0\) thì \(U_{Lmax}\), khi đó: \(\frac{1}{\omega_0^2}=\frac{1}{\omega_1^2}+\frac{1}{\omega_2^2}\)(2)
Theo giả thiết, ta có \(\frac{1}{\omega_0^2}=\frac{1}{266,6^2}+\frac{1}{355,4^2}\)\(\Rightarrow\omega_0=213,3\) rad/s.
Thay vào (1) ta có: \(213,3=\frac{1}{6,63.10^{-5}\sqrt{\frac{1,99}{6,63.10^{-5}}-\frac{R^2}{2}}}\)\(\Rightarrow R=150\sqrt{2}\Omega\)
Đáp án B.
Có lỗi một chút, ở công thức (2) các bạn sửa lại thế này mới đúng: \(\frac{2}{\omega_0^2}=\frac{1}{\omega_1^2}+\frac{1}{\omega_2^2}\)
Rồi tính tương tự ta được \(R=150\sqrt{2}\)
Vật thực hiện 10 dao động mất 20s:
\(T=\frac{t}{n}=2s\Rightarrow g=4\pi^2\frac{l}{T^2}=9,86m/s^2\)
Đáp án C
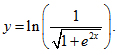
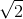
1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=(x2−2)e2xy=(x2−2)e2x trên đoạn [−3;1][−3;1]
Để tìm giá trị lớn nhất và nhỏ nhất của hàm số trên một đoạn, ta thực hiện các bước sau:
Ta có: y′=(2x)e2x+(x2−2)(2e2x)=(2x2+2x−4)e2xy′=(2x)e2x+(x2−2)(2e2x)=(2x2+2x−4)e2x
(2x2+2x−4)e2x=0(2x2+2x−4)e2x=0 Vì e2x>0e2x>0 với mọi xx, nên ta chỉ cần giải phương trình 2x2+2x−4=02x2+2x−4=0. Giải phương trình bậc hai này, ta được x=1x=1 hoặc x=−2x=−2.
So sánh các giá trị 7e−67e−6, 2e−42e−4, và −e2−e2. Ta thấy:
2. Cho hàm số y=ln(121+e−−−−√)y=ln(121+e). Chứng minh e2y−y′=1e2y−y′=1
Vì y=ln(121+e−−−−√)y=ln(121+e), ta thấy yy là một hằng số vì không phụ thuộc vào xx. Do đó, y′=0y′=0.
e2y=e2ln(121+e√)=eln((121+e√)2)=eln(1+e4)=1+e4e2y=e2ln(121+e)=eln((121+e)2)=eln(1+e4)=1+e4
Ta có: e2y−y′=1+e4−0=1+e4e2y−y′=1+e4−0=1+e4. Tuy nhiên, đề bài yêu cầu chứng minh e2y−y′=1e2y−y′=1. Có vẻ như có một sự nhầm lẫn trong đề bài hoặc trong cách tính toán.
Nếu đề bài đúng là y=12ln(1+e)y=12ln(1+e), thì: y′=0y′=0 e2y=e2.12ln(1+e)=eln(1+e)=1+ee2y=e2.12ln(1+e)=eln(1+e)=1+e e2y−y′=1+e−0=1+ee2y−y′=1+e−0=1+e
Hoặc nếu đề bài là y=12ln(1+e4)y=12ln(1+e4), thì: y′=0y′=0 e2y=e2.12ln(1+e4)=eln(1+e4)=1+e4e2y=e2.12ln(1+e4)=eln(1+e4)=1+e4 e2y−y′=1+e4−0=1+e4e2y−y′=1+e4−0=1+e4
Như vậy, với đề bài đã cho, không thể chứng minh được e2y−y′=1e2y−y′=1.