Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Từ giả thiết ta có: \(a = 3,c = 5 \Rightarrow b = \sqrt {{c^2} - {a^2}} = \sqrt {{5^2} - {3^2}} = 4\)
Ta có phương trình chính tắc của hypebol là: \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\)
b) Ta có: \(2a = 8,2b = 6 \Rightarrow a = 4,b = 3\)
Suy ra phương trình chính tắc của hypebol là \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)

Phương trình chính tắc của elip có dạng :
+
= 1
a) Ta có a > b :
2a = 8 => a = 4 => a2 = 16
2b = 6 => b = 3 => b2 = 9
Vậy phương trình chính tắc của elip có dạng +
= 1
b) Ta có: 2a = 10 => a = 5 => a2 = 25
2c = 6 => c = 3 => c2 = 9
=> b2 = a2 – c2 => b2 = 25 – 9 = 16
Vậy phương trình chính tắc của elip có dạng +
= 1

Chọn B
Ta có a = 4 2 c = 10 b 2 = c 2 - a 2 ⇒ a = 4 c = 5 b = 3
Phương trình chính tắc của Hyperbol là
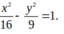

Đáp án: C
Ta có:
2a = 8 ⇒ a = 4 ⇒ a 2 = 16
2b = 6 ⇒ b = 3 ⇒ b 2 = 9
Vậy phương trình chính tắc của elip là:
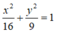

Độ dài trục lớn bằng 8 ⇒ 2a = 8 ⇒ a = 4
Độ dài trục nhỏ bằng 6 ⇒ 2b = 6 ⇒ b = 3
Vậy phương trình chính tắc của Elip là: 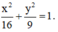

Phương trình chính tắc của elip có dạng :
+
= 1
a) Ta có a > b :
2a = 8 => a = 4 => a2 = 16
2b = 6 => b = 3 => b2 = 9
Vậy phương trình chính tắc của elip có dạng +
= 1
b) Ta có: 2a = 10 => a = 5 => a2 = 25
2c = 6 => c = 3 => c2 = 9
=> b2 = a2 – c2 => b2 = 25 - 9 = 16
Vậy phương trình chính tắc của elip có dạng +
= 1.

Đáp án: D
Ta có:
2a = 8 ⇒ a = 4
2c = 6 ⇒ c = 3
Mà b 2 = a 2 - c 2 = 16 - 9 = 7
Suy ra, phương trình elip cần tìm là:
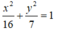

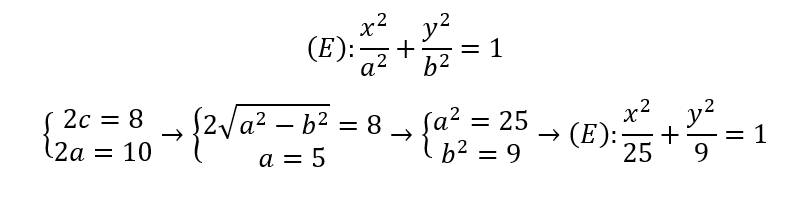
Có hai dạng chính tắc của hyperbol:
\(\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 \Rightarrow \frac{x^{2}}{16} - \frac{y^{2}}{4} = 1\)
\(\frac{y^{2}}{a^{2}} - \frac{x^{2}}{b^{2}} = 1 \Rightarrow \frac{y^{2}}{16} - \frac{x^{2}}{4} = 1\)
Kết luận:
Vì đề nói rõ "trục thực là 8", tức trục thực = 2a = 8 → a = 4
và "trục ảo là 4" → 2b = 4 → b = 2
→ Phương trình chính tắc của hyperbol là:
\(\frac{x^{2}}{16} - \frac{y^{2}}{4} = 1\)
(Nếu trục thực là trục hoành — tức hypebol nằm ngang)