Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 6:
Để B là số nguyên thì \(\sqrt{x}-2+3⋮\sqrt{x}-2\)
\(\Leftrightarrow\sqrt{x}-2\in\left\{1;-1;3\right\}\)
hay \(x\in\left\{9;1;25\right\}\)

\(\Leftrightarrow6\sqrt{x}-9+10⋮2\sqrt{x}-3\)
=>\(2\sqrt{x}-3\in\left\{1;-1;2;-2;5;-5;10;-10\right\}\)
hay \(x\in\left\{4;1;16\right\}\)

\(\left(\sqrt{x}-6\right)\left(x-1\right)=0=>\int^{\sqrt{x}-6=0}_{x-1=0}=>\int^{\sqrt{x}=6}_{x=1}=>x=\left\{36;1\right\}\)
căn x-1=3=>căn x =4 =>x=4^2=16
x^3-2x=0 =>x(x^2-2)=0 =>x=0 hoặc x^2-2=0=>x=0 hoặc x^2=2 =>...
các câu sau tương tự

a) Ta có : \(x=\sqrt{40+2}=\sqrt{42}< \sqrt{49}=7\) (1)
\(y=\sqrt{40}+\sqrt{2}>\sqrt{36}+\sqrt{1}=6+1=7\) (2)
Từ (1) và (2) => x = y
b) Ta có : \(x=\sqrt{625}-\frac{1}{\sqrt{5}}=25-\frac{1}{\sqrt{5}}\) (1)
\(y=\sqrt{576}-\frac{1}{\sqrt{6}}+1=24-\frac{1}{\sqrt{6}}+1=25-\frac{1}{\sqrt{6}}\) (2)
Vì \(\sqrt{5}< \sqrt{6}\)nên \(\frac{1}{\sqrt{5}}>\frac{1}{\sqrt{6}}\)(3)
(1),(2),(3) => \(x>y\)
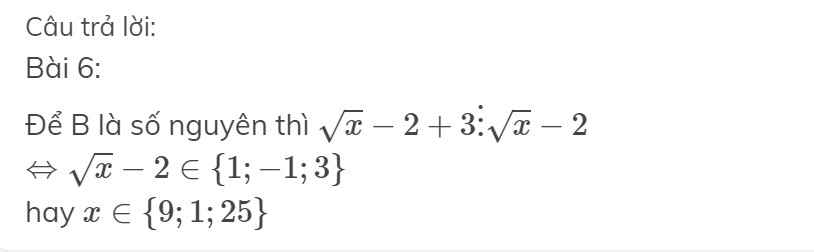
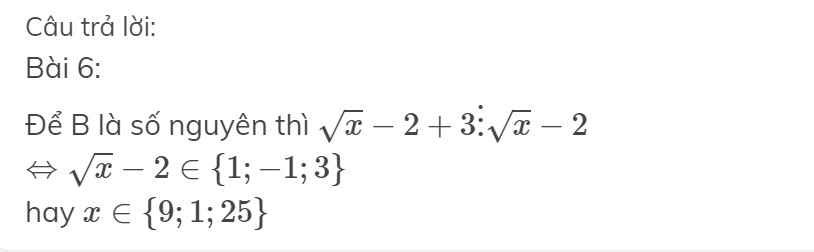
Ta có: \(B=\left(\dfrac{x-6}{x+3\sqrt{x}}-\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{x}+3}\right)\cdot\dfrac{2\sqrt{x}-6}{\sqrt{x}}\)
\(=\dfrac{x-6-\left(\sqrt{x}+3\right)+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+3\right)}\cdot\dfrac{2\left(\sqrt{x}-3\right)}{\sqrt{x}}\)
\(=\dfrac{x-6+\sqrt{x}-\sqrt{x}-3}{\left(\sqrt{x}+3\right)\cdot\sqrt{x}}\cdot\dfrac{2\left(\sqrt{x}-3\right)}{\sqrt{x}}\)
\(=\dfrac{x-9}{\sqrt{x}+3}\cdot\dfrac{2\left(\sqrt{x}-3\right)}{x}=\dfrac{\left(\sqrt{x}-3\right)\cdot2\left(\sqrt{x}-3\right)}{x}\)
\(=\dfrac{2\left(\sqrt{x}-3\right)^2}{x}\)
j ạ