Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có \(\frac{d\left(A,\left(SCD\right)\right)}{d\left(M,\left(SCD\right)\right)}=2\Rightarrow d=\left(m,\left(SCD\right)\right)=\frac{1}{2}d\left(A,\left(SCD\right)\right)\)
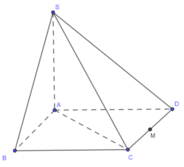
Dễ thấy AC _|_ CD, SA _|_ CD dựng AH _|_ SA => AH _|_ (SCD)
Vậy d(A,(SCD))=AH
Xét tam giác vuông SAC (A=1v) có \(\frac{1}{AH^2}=\frac{1}{AC^2}+\frac{1}{AS^2}\Rightarrow AH=\frac{a\sqrt{6}}{3}\)
Vậy suy ra \(d\left(M,\left(SCD\right)\right)=\frac{a\sqrt{6}}{3}\)
.jpg)
E=AB∩CD,G=EN∩SB⇒GE=AB∩CD,G=EN∩SB⇒G là trọng tâm tam giác SAE.
d(M,(NCD))=GMGBd(B,(NCD))=12d(B,(NCD))=12.12d(A,(NCD))=14d(A,(NCD))=14hd(M,(NCD))=GMGBd(B,(NCD))=12d(B,(NCD))=12.12d(A,(NCD))=14d(A,(NCD))=14h
Tứ diện AEND vuông tại đỉnh A nên 1h2=1AN2+1AE2+1AD2=116a2⇒h=a√66111h2=1AN2+1AE2+1AD2=116a2⇒h=a6611
Vậy d(M,(NCD))=a√6644.d(M,(NCD))=a6644.
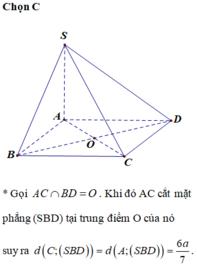
Chọn C
Phương pháp:
- Xác định góc giữa mặt phẳng (SBD) với (ABD) (góc giữa hai đường thẳng cùng vuông góc với giao tuyến)
- Tính khoảng cách dựa vào công thức tỉ số khoảng cách:
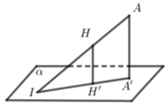
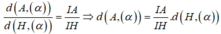
Cách giải
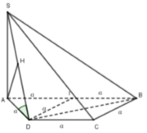
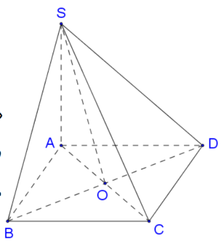
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Từ A kẻ \(AH\perp SO\Rightarrow AH\perp\left(SBD\right)\)
\(\Rightarrow AH=d\left(A;\left(SBD\right)\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng: \(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AO^2}\Rightarrow AH=\dfrac{SA.AO}{\sqrt{SA^2+AO^2}}=\dfrac{a\sqrt{21}}{7}\)
Chọn A.
Xác định được
Vì M là trung điểm SA nên
Kẻ AK ⊥ DM và chứng minh được AK ⊥ (CDM) nên
Trong tam giác vuông MAD tính được
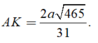
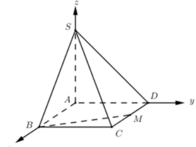
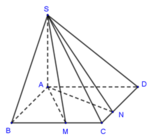
Bước 1: Xác định tọa độ các điểm trong không gian
Giả sử:
Bước 2: Tính tọa độ của trung điểm \(M\) của cạnh \(C D\)
Trung điểm \(M\) của cạnh \(C D\) có tọa độ trung bình của \(C\) và \(D\):
\(M = \left(\right. \frac{a + 0}{2} , \frac{a + a}{2} , \frac{0 + 0}{2} \left.\right) = \left(\right. \frac{a}{2} , a , 0 \left.\right)\)
Bước 3: Xác định phương trình mặt phẳng \(\left(\right. S B D \left.\right)\)
Để xác định phương trình mặt phẳng \(\left(\right. S B D \left.\right)\), ta cần ba điểm \(S\), \(B\), và \(D\). Tính vectơ chỉ phương của hai đoạn thẳng \(S B\) và \(B D\):
Tính tích có hướng của hai vectơ \(\overset{\rightarrow}{S B}\) và \(\overset{\rightarrow}{B D}\):
\(\overset{\rightarrow}{S B} \times \overset{\rightarrow}{B D} = \mid \hat{i} & \hat{j} & \hat{k} \\ \frac{a}{2} & - \frac{a}{2} & - 2 a \\ - a & a & 0 \mid\)
Tính toán:
\(\overset{\rightarrow}{S B} \times \overset{\rightarrow}{B D} = \hat{i} \left(\right. \left(\right. - \frac{a}{2} \left.\right) \cdot 0 - \left(\right. - 2 a \left.\right) \cdot a \left.\right) - \hat{j} \left(\right. \frac{a}{2} \cdot 0 - \left(\right. - 2 a \left.\right) \cdot \left(\right. - a \left.\right) \left.\right) + \hat{k} \left(\right. \frac{a}{2} \cdot a - \left(\right. - \frac{a}{2} \left.\right) \cdot \left(\right. - a \left.\right) \left.\right)\) \(= \hat{i} \left(\right. 2 a^{2} \left.\right) - \hat{j} \left(\right. 2 a^{2} \left.\right) + \hat{k} \left(\right. \frac{a^{2}}{2} - \frac{a^{2}}{2} \left.\right)\) \(= 2 a^{2} \hat{i} - 2 a^{2} \hat{j} + 0 \hat{k}\) \(= \left(\right. 2 a^{2} , - 2 a^{2} , 0 \left.\right)\)
Vậy vectơ pháp tuyến của mặt phẳng \(\left(\right. S B D \left.\right)\) là \(\left(\right. 2 a^{2} , - 2 a^{2} , 0 \left.\right)\).
Phương trình mặt phẳng \(\left(\right. S B D \left.\right)\) có dạng:
\(2 a^{2} \left(\right. x - \frac{a}{2} \left.\right) - 2 a^{2} \left(\right. y - \frac{a}{2} \left.\right) = 0\) \(2 a^{2} x - a^{2} - 2 a^{2} y + a^{2} = 0\) \(2 a^{2} x - 2 a^{2} y = 0\) \(x = y\)
Bước 4: Tính khoảng cách từ \(M\) đến mặt phẳng \(\left(\right. S B D \left.\right)\)
Khoảng cách từ điểm \(M \left(\right. x_{0} , y_{0} , z_{0} \left.\right) = \left(\right. \frac{a}{2} , a , 0 \left.\right)\) đến mặt phẳng \(a x + b y + c z + d = 0\) được tính theo công thức:
\(d = \frac{\mid a x_{0} + b y_{0} + c z_{0} + d \mid}{\sqrt{a^{2} + b^{2} + c^{2}}}\)
Với phương trình mặt phẳng \(x - y = 0\), ta có \(a = 1 , b = - 1 , c = 0 , d = 0\). Thay vào công thức:
\(d = \frac{\mid 1 \cdot \frac{a}{2} - 1 \cdot a + 0 \cdot 0 + 0 \mid}{\sqrt{1^{2} + \left(\right. - 1 \left.\right)^{2} + 0^{2}}} = \frac{\mid \frac{a}{2} - a \mid}{\sqrt{2}} = \frac{\mid - \frac{a}{2} \mid}{\sqrt{2}} = \frac{\frac{a}{2}}{\sqrt{2}} = \frac{a}{2 \sqrt{2}}\)
Kết quả
Khoảng cách từ trung điểm \(M\) của cạnh \(C D\) đến mặt phẳng \(\left(\right. S B D \left.\right)\) là \(\frac{a}{2 \sqrt{2}}\).
TICK CHO MK NHA!
Gọi E là giao điểm của AM và BD
Áp dụng định lý Thales:
\(\dfrac{EM}{AE}=\dfrac{DM}{AB}=\dfrac{1}{2}\) (do M là trung điểm CD)
\(\Rightarrow EM=\dfrac{1}{2}AE\)
Mà \(AM\cap\left(SBD\right)=E\Rightarrow d\left(M;\left(SBD\right)\right)=\dfrac{1}{2}d\left(A;\left(SBD\right)\right)\)
Gọi O là giao điểm AC và BD \(\Rightarrow AC\perp BD\) tại O theo t/c hình vuông
Trong tam giác SAO, từ A kẻ \(AH\perp SO\) (1)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\AC\perp BD\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
\(\Rightarrow BD\perp AH\) (2)
(1);(2) \(\Rightarrow AH\perp\left(SBD\right)\Rightarrow AH=d\left(A;\left(SBD\right)\right)\)
\(AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
Áp dụng hệ thức lượng: \(AH=\dfrac{SA.AO}{\sqrt{SA^2+AO^2}}=\dfrac{2}{3}\)
\(\Rightarrow d\left(M;\left(SBD\right)\right)=\dfrac{1}{2}AH=\dfrac{1}{3}\)