K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
20 tháng 5 2018
a) Đặt \(A=\frac{7^{15}}{1+7+7^2+...+7^{14}}\)
Đặt \(B=1+7+7^2+...+7^{14}\)
\(\Rightarrow7B=7+7^2+...+7^{15}\)
\(\Rightarrow7B-B=6B=7^{15}-1\)
\(\Rightarrow B=\frac{7^{15}-1}{6}\)
\(\Rightarrow A=\frac{7^{15}-1+1}{\frac{7^{15}-1}{6}}=\left(7^{15}-1\right).\frac{6}{7^{15}-1}+\frac{6}{7^{15}-1}=6+\frac{6}{7^{15}-1}\)
Tự làm tiếp nha
2 tháng 5 2019
a) A=\(\frac{178}{179}+\frac{179}{180}+\frac{183}{181}\)
ta có :
\(A=\left(1-\frac{1}{179}\right)+\left(1-\frac{1}{180}\right)+\left(1+\frac{2}{181}\right)\)
\(\Rightarrow A=\left(1+1+1\right)-\left(\frac{1}{179}-\frac{1}{180}+\frac{2}{181}\right)\)
\(\Rightarrow A=3-\left(\frac{1}{179}-\frac{1}{180}+\frac{2}{181}\right)< 3\)
Vậy \(A< 3\)
KN
2 tháng 5 2019
a. Ta có :
\(\frac{178}{179}< 1\left(\frac{1}{179}\right)\)
\(\frac{179}{180}< 1\left(\frac{1}{180}\right)\)
\(\frac{183}{181}>1\left(\frac{3}{181}\right)\left(1\right)\)
Mà \(\frac{3}{181}>\frac{1}{179}+\frac{1}{180}\left(=\frac{359}{32220}< \frac{3}{181}\right)\left(2\right)\)
Từ \(\left(1\right)\&\left(2\right)\Rightarrow\frac{178}{179}+\frac{179}{180}+\frac{183}{181}< 1+1+1\)
Vậy \(A< 3\)
31 tháng 12 2017
A = 1 + 7^9/1+7+7^2+....+7^8
= 1 + 7^9-1/1+7+....+7^8 + 1/1+7+....+1/7^8
= 1 + 7-1 + 1/1+7+....+7^8
= 7 + 1/1+7+....+7^8
Tương tự : B = 5 + 1/1+5+....+5^8
Vì 1/1+5+.....+5^8 < 1 => B < 5+1 = 6
Mà A > 6 => A > B
k mk nha
25 tháng 3 2019
ta có : A = \(\frac{7^{10}}{1+7+7^2+7^3+...+7^9}=1:\frac{1+7+7^2+7^3+...+7^9}{7^{10}}\)
= \(1:\left(\frac{1}{7^{10}}+\frac{7}{7^{10}}+\frac{7^2}{7^{10}}+...+\frac{7^8}{7^{10}}+\frac{7^9}{7^{10}}\right)\)=\(1:\left(\frac{1}{7^{10}}+\frac{1}{7^9}+\frac{1}{7^8}+...+\frac{1}{7^2}+\frac{1}{7}\right)\)
tương tự ta được : B = \(1:\left(\frac{1}{5^{10}}+\frac{1}{5^9}+\frac{1}{5^8}+...+\frac{1}{5^2}+\frac{1}{5}\right)\)
Vì \(\frac{1}{7^{10}}+\frac{1}{7^9}+\frac{1}{7^8}+...+\frac{1}{7^2}+\frac{1}{7}\)< \(\frac{1}{5^{10}}+\frac{1}{5^9}+\frac{1}{5^8}+...+\frac{1}{5^2}+\frac{1}{5}\)
=> A > B
PN
18 tháng 7 2017
a) \(6\dfrac{5}{7}-\left(1\dfrac{3}{4}+2\dfrac{5}{7}\right)\)
\(=6\dfrac{5}{7}-1\dfrac{3}{4}-2\dfrac{5}{7}\)
\(=\left(6\dfrac{5}{7}-2\dfrac{5}{7}\right)-1\dfrac{3}{4}\)
\(=4-1\dfrac{3}{4}\)
\(=3\dfrac{3}{4}\)
PN
18 tháng 7 2017
b) \(7\dfrac{5}{11}-\left(2\dfrac{3}{7}+3\dfrac{5}{11}\right)\)
\(=7\dfrac{5}{11}-2\dfrac{3}{7}-3\dfrac{5}{11}\)
\(=\left(7\dfrac{5}{11}-3\dfrac{5}{11}\right)-2\dfrac{3}{7}\)
\(=4-2\dfrac{3}{7}\)
\(=2\dfrac{3}{7}\)
23 tháng 7 2020
Bài 1:
a) Ta có: \(6\frac{5}{7}-\left(1\frac{3}{4}+2\frac{5}{7}\right)\)
\(=6\frac{5}{7}-1\frac{3}{4}-2\frac{5}{7}\)
\(=4\frac{5}{7}-1\frac{3}{4}\)
\(=\frac{33}{7}-\frac{7}{4}\)
\(=\frac{132}{28}-\frac{49}{28}=\frac{83}{28}\)
b) Ta có: \(7\frac{5}{9}-\left(2\frac{3}{4}+3\frac{5}{9}\right)\)
\(=7\frac{5}{9}-2\frac{3}{4}-3\frac{5}{9}\)
\(=4\frac{5}{9}-2\frac{3}{4}\)
\(=\frac{41}{9}-\frac{11}{4}\)
\(=\frac{164}{36}-\frac{99}{36}=\frac{65}{36}\)
c) Ta có: \(\frac{-3}{5}\cdot\frac{5}{7}+\frac{-3}{5}\cdot\frac{3}{7}+\frac{-3}{5}\cdot\frac{6}{7}\)
\(=\frac{-3}{5}\cdot\left(\frac{5}{7}+\frac{3}{7}+\frac{6}{7}\right)\)
\(=\frac{-3}{5}\cdot2=-\frac{6}{5}\)
d) Ta có: \(\frac{1}{3}\cdot\frac{4}{5}+\frac{1}{3}\cdot\frac{6}{5}-\frac{4}{3}\)
\(=\frac{1}{3}\cdot\frac{4}{5}+\frac{1}{3}\cdot\frac{6}{5}-\frac{1}{3}\cdot4\)
\(=\frac{1}{3}\left(\frac{4}{5}+\frac{6}{5}-4\right)\)
\(=\frac{1}{3}\cdot\left(-2\right)=\frac{-2}{3}\)
12 tháng 6 2018
b, Ta có:\(\dfrac{1+3+3^2+.....+3^{10}}{1+3+3^2+.....+3^9}\) \(=\dfrac{1}{1+3+3^2+...+3^9}+\dfrac{3+3^2+...+3^{10}}{1+3+3^2+...+3^9}\)\(=\dfrac{1}{1+3+3^2+...+3^9}+\dfrac{3.\left(1+3+3^2+...+3^9\right)}{1+3+3^2+...+3^9}\)
\(=\dfrac{1}{1+3+3^2+...+3^9}+3< 4\)
\(\Rightarrow\) \(\dfrac{1+3+3^2+...+3^{10}}{1+3+3^2+...+3^9}< 4\) \(\left(1\right)\)
Ta có :\(\dfrac{1+5+5^2+...+5^{10}}{1+5+5^2+...+5^9}\)
\(=\dfrac{1}{1+5+5^2+...+5^9}+\dfrac{5+5^2+...+5^{10}}{1+5+5^2+....+5^9}\)
\(=\dfrac{1}{1+5+5^2+...+5^9}+\dfrac{5.\left(1+5+5^2+...+5^9\right)}{1+5+5^2+...+5^9}\)
\(=\dfrac{1}{1+5+5^2+...+5^9}+5>5\)
\(\Rightarrow\) \(\dfrac{1+5+5^2+...+5^{10}}{1+5+5^2+...+5^9}>5\) \(\left(2\right)\)
Từ \(\left(1\right)và\left(2\right)\)
\(\Rightarrow\dfrac{1+3+3^2+...+3^{10}}{1+3+3^2+...+3^9}< \dfrac{1+5+5^2+...+5^{10}}{1+5+5^2+...+5^9}\)
Vậy \(\dfrac{1+3+3^2+...+3^{10}}{1+3+3^2+...+3^9}< \dfrac{1+5+5^2+...+5^{10}}{1+5+5^2+...+5^9}\)
12 tháng 6 2018
a, Đặt \(A\)\(=\dfrac{7^{15}}{1+7+7^2+...+7^{14}}\)
\(\Rightarrow\) \(\dfrac{1}{A}\) \(=\dfrac{1+7+7^2+...+7^{14}}{7^{15}}=\dfrac{1}{7^{15}}+\dfrac{7}{7^{15}}+\dfrac{7^2}{7^{15}}+...+\dfrac{7^{14}}{7^{15}}\)
\(=\dfrac{1}{7^{15}}+\dfrac{1}{7^{14}}+\dfrac{1}{7^{13}}+....+\dfrac{1}{7}\)
Đặt \(B=\dfrac{9^{15}}{1+9+9^2+...+9^{14}}\)
\(\Rightarrow\dfrac{1}{B}=\dfrac{1+9+9^2+...+9^{14}}{9^{15}}=\dfrac{1}{9^{15}}+\dfrac{9}{9^{15}}+\dfrac{9^2}{9^{15}}+...+\dfrac{9^{14}}{9^{15}}\)
\(=\dfrac{1}{9^{15}}+\dfrac{1}{9^{14}}+\dfrac{1}{9^{13}}+...+\dfrac{1}{9}\)
Mà \(\dfrac{1}{7^{15}}>\dfrac{1}{9^{15}};\dfrac{1}{7^{14}}>\dfrac{1}{9^{14}};\dfrac{1}{7^{13}}>\dfrac{1}{9^{13}};....;\dfrac{1}{7}>\dfrac{1}{9}\)
\(\Rightarrow\dfrac{1}{A}>\dfrac{1}{B}\) \(\Rightarrow A< B\)
Vậy\(\dfrac{7^{15}}{1+7+7^2+...+7^{14}}>\dfrac{9^{15}}{1+9+9^2+....+9^{14}}\)
PT
26 tháng 4 2017
kazuto kirigaya thật là bt làm ko đó ko bt thì nói đi còn bt thì làm đi
Q
17 tháng 4 2017
\(A=11\dfrac{3}{13}-\left(2\dfrac{4}{7}+5\dfrac{3}{13}\right)\)
\(A=11\dfrac{3}{13}-5\dfrac{3}{13}-2\dfrac{4}{7}\)
\(A=6-2\dfrac{4}{7}\)
\(A=5\dfrac{7}{7}-2\dfrac{4}{7}\)
\(A=3\dfrac{3}{7}\)
\(B=\left(6\dfrac{4}{9}+3\dfrac{7}{11}\right)-4\dfrac{4}{9}\)
\(B=\left(6\dfrac{4}{9}-4\dfrac{4}{9}\right)+3\dfrac{7}{11}\)
\(B=2+3\dfrac{7}{11}\)
\(B=5\dfrac{7}{11}\)
\(C=\dfrac{-5}{7}.\dfrac{2}{11}+\dfrac{-5}{7}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-5}{7}.\left(\dfrac{2}{11}+1\right)-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-5}{7}.\dfrac{13}{11}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-65}{77}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{4}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{160}{11}\)
\(D=0,7.2\dfrac{2}{3}.20.0,375.\dfrac{5}{28}\)
\(D=\dfrac{7}{10}.\dfrac{8}{3}.20.\dfrac{375}{1000}.\dfrac{5}{28}\)
\(D=\dfrac{7}{28}=\dfrac{5}{2}\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{3}-0,25-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{3}-\dfrac{1}{4}-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{12}-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right).0\)
\(\Rightarrow E=0\)
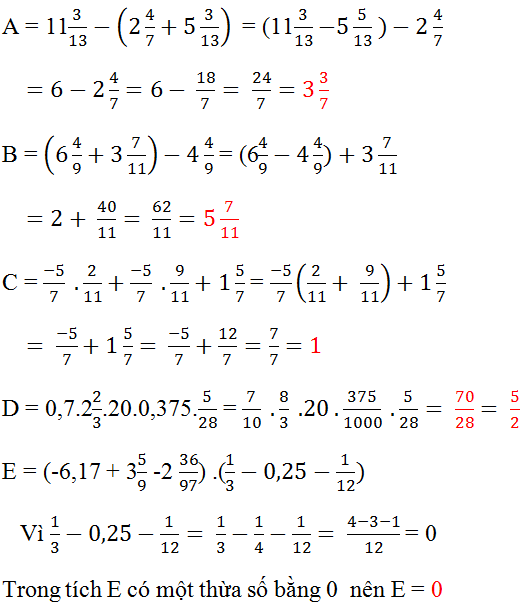
yêu cầu đề bài là gì thế bạn
3 nhân 3 phần 5 và 7 = 1 phần 5