K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 8
a: Ta có: \(\hat{AOD}+\hat{BOD}=180^0\) (hai góc kề bù)
=>\(\hat{BOD}=180^0-97^0=83^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OA, ta có: \(\hat{AOE}<\hat{AOD}\left(56^0<97^0\right)\)
nên tia OE nằm giữa hai tia OA và OD
=>\(\hat{AOE}+\hat{EOD}=\hat{AOD}\)
=>\(\hat{EOD}=97^0-56^0=41^0\)
Ta có: \(\hat{AOE}+\hat{EOC}+\hat{COB}=180^0\)
=>\(\hat{EOC}=180^0-56^0-42^0=82^0\)
b: Trên cùng một nửa mặt phẳng bờ chứa tia OE, ta có; \(\hat{EOD}<\hat{EOC}\left(41^0<82^0\right)\)
nên tia OD nằm giữa hai tia OE và OC
=>\(\hat{EOD}+\hat{DOC}=\hat{EOC}\)
=>\(\hat{DOC}=82^0-41^0=41^0\)
Ta có: tia OD nằm giữa hai tia OE và OC
\(\hat{DOE}=\hat{DOC}\left(=41^0\right)\)
Do đó: OD là phân giác của góc EOC
14 tháng 8
a: ||\(x:\left(-\frac23\right)+\frac12\) |+\(\frac56\) |\(\cdot\frac12=\frac34\)
=>||\(x:\left(-\frac23\right)+\frac12\) |\(+\frac56\) |\(=\frac34:\frac12=\frac32\)
mà \(\left|x:\left(-\frac23\right)+\frac12\right|+\frac56\ge\frac56\)
nên \(\left|x:\left(-\frac23\right)+\frac12\right|+\frac56=\frac32\)
=>\(\left|x:\left(-\frac23\right)+\frac12\right|=\frac32-\frac56=\frac96-\frac56=\frac46=\frac23\)
=>\(\left[\begin{array}{l}x:\left(-\frac23\right)+\frac12=\frac23\\ x:\left(-\frac23\right)+\frac12=-\frac23\end{array}\right.\Rightarrow\left[\begin{array}{l}x:\left(-\frac23\right)=\frac23-\frac12=\frac16\\ x:\left(-\frac23\right)=-\frac23-\frac12=-\frac46-\frac36=-\frac76\end{array}\right.\)
=>\(\left[\begin{array}{l}x=\frac16\cdot\left(-\frac23\right)=-\frac{2}{18}=-\frac19\\ x=-\frac76\cdot\left(-\frac23\right)=\frac{14}{18}=\frac79\end{array}\right.\)
a: \(\left|-\frac23x+\frac38\right|\cdot\left(-\frac85\right)=-\frac{8}{15}\)
=>\(\left|\frac23x-\frac38\right|=\frac{8}{15}:\frac85=\frac{5}{15}=\frac13\)
=>\(\left[\begin{array}{l}\frac23x-\frac38=\frac13\\ \frac23x-\frac38=-\frac13\end{array}\right.\Rightarrow\left[\begin{array}{l}\frac23x=\frac38+\frac13=\frac{17}{24}\\ \frac23x=-\frac13+\frac38=\frac{1}{24}\end{array}\right.\)
=>\(\left[\begin{array}{l}x=\frac{17}{24}:\frac23=\frac{17}{24}\cdot\frac32=\frac{17}{16}\\ x=\frac{1}{24}:\frac23=\frac{1}{24}\cdot\frac32=\frac{3}{48}=\frac{1}{16}\end{array}\right.\)
S
subjects
CTVHS
14 tháng 8
\(a.x:\left(-\frac23\right)-\frac12\left|+\frac56\right|\cdot\frac12=\frac34\)
\(x\cdot\left(-\frac32\right)-\frac12+\frac{5}{12}=\frac34\)
\(x\cdot\left(-\frac32\right)=\frac34-\frac{5}{12}+\frac12\)
\(x\cdot\left(-\frac32\right)=\frac56\)
\(x=\frac56:\left(-\frac32\right)=\frac56\cdot\left(-\frac23\right)\)
\(x=-\frac59\)
\(b.\left(-\frac23\right)x+\frac38\cdot\left(-\frac85\right)=-\frac{8}{15}\)
\(\left(-\frac23\right)x-\frac35=-\frac{8}{15}\)
\(\left(-\frac23\right)x=-\frac{8}{15}+\frac35=\frac{1}{15}\)
\(x=\frac{1}{15}:\left(-\frac23\right)=\frac{1}{15}\cdot\left(-\frac32\right)\)
\(x=-\frac{1}{10}\)
11 tháng 8
Bài 2:
Qua B, kẻ tia BD nằm giữa hai tia BA và BC sao cho BD//Ax//Cz
ta có: BD//Ax
=>\(\hat{xAB}+\hat{ABD}=180^0\) (hai góc trong cùng phía)
=>\(\hat{ABD}=180^0-125^0=55^0\)
Ta có: BD//Cz
=>\(\hat{DBC}+\hat{BCz}=180^0\) (hai góc trong cùng phía)
=>\(\hat{DBC}=180^0-130^0=50^0\)
Ta có: tia BD nằm giữa hai tia BA và BC
=>\(\hat{ABC}=\hat{DBA}+\hat{DBC}\)
=>\(\hat{ABC}=55^0+50^0=105^0\)
Bài 3:
Ax//yy'
=>\(\hat{xAB}=\hat{yBA}\) (hai góc so le trong)
=>\(\hat{yBA}=50^0\)
Cz//yy'
=>\(\hat{yBC}=\hat{zCB}\) (hai góc so le trong)
=>\(\hat{yBC}=40^0\)
Ta có: tia By nằm giữa hai tia BA và BC
=>\(\hat{ABC}=\hat{yBA}+\hat{yBC}=40^0+50^0=90^0\)
Bài 4:
Qua B, kẻ tia BD nằm giữa hai tia BA và BC sao cho BD//Ax//Cz
BD//Ax
=>\(\hat{xAB}+\hat{ABD}=180^0\) (hai góc trong cùng phía)
=>\(\hat{ABD}=180^0-110^0=70^0\)
ta có; tia BD nằm giữa hai tia BA và BC
=>\(\hat{DBA}+\hat{DBC}=\hat{ABC}\)
=>\(\hat{DBC}=100^0-70^0=30^0\)
Ta có: \(\hat{DBC}=\hat{zCB}\left(=30^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên BD//Cz
Ta có: BD//Ax
BD//Cz
Do đó: Ax//Cz
11 tháng 8
a: a//b
=>\(\hat{A_1}=\hat{B_3}\) (hai góc so le trong)
mà \(\hat{A_1}=65^0\)
nên \(\hat{B_3}=65^0\)
b: Ta có: \(\hat{B}_3+\hat{B_2}=180^0\) (hai góc kề bù)
=>\(\hat{B_2}=180^0-65^0=115^0\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
11 tháng 8
Giải:
a; \(\hat{A_1}\) = \(65^0\) (gt)
\(\hat{A_1}\) = \(\hat{A_3}\) = 65\(^0\)(đối đỉnh)
\(\hat{A_3}\) = \(\hat{B_3}\) = \(65^0\) (slt)
b; \(\hat{B_2}\) + \(\hat{B_3}\) = 180\(^0\) (hai góc kề bù)
\(\hat{B_2}\) = 180\(^0\) - \(\hat{B_3}\)
\(\hat{B_2}\) = 180\(^0\) - 65\(^0\) = 115\(^0\)
Vậy a; \(\hat{B}_3\) = 65\(^0\)
b; \(\hat{B_2}\) = 115\(^0\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 9
4.
Ta có: \(S=2^1+3^{4.1+1}+4^{4.2+1}+\cdots+2024^{4.2002+1}\)
Do tính chất lũy thừa bậc 4n+1 của 1 số có tận cùng giống số đó, nên S có cùng chữ số tận cùng với tổng:
\(S_1=2+3+4+\cdots+2024=\frac{2024.2025}{2}-1=2049299\)
Vậy S có tận cùng bằng 9
BM
1
10 tháng 8
Bài 1:
a: \(A\left(x\right)=5x^4-7x^2-3x-6x^2+11x-30\)
\(=5x^4-7x^2-6x^2-3x+11x-30\)
\(=5x^4-13x^2+8x-30\)
\(B=-11x^3+5x-10+5x^4-2+20x^3-34x\)
\(=5x^4+20x^3-11x^3+5x-34x-2-10\)
\(=5x^4+9x^3-29x-12\)
b: A(x)+B(x)
\(=5x^4-13x^2+8x-30+5x^4+9x^3-29x-12\)
\(=10x^4-4x^3-21x-42\)
A(x)-B(x)
\(=5x^4-13x^2+8x-30-5x^4-9x^3+29x+12\)
\(=-9x^3-13x^2+37x-18\)
Bài 2:
a: \(M=2x^2+5x-12\)
Bậc là 2
Hệ số cao nhất là 2
Hệ số tự do là -12
b: M+N
\(=2x^2+5x-12+x^2-8x-1=3x^2-3x-13\)
c: P(2x-3)=M
=>\(P=\frac{2x^2+5x-12}{2x-3}=\frac{2x^2-3x+8x-12}{2x-3}\)
\(=\frac{x\left(2x-3\right)+4\left(2x-3\right)}{2x-3}\)
=x+4
20 tháng 8
Ta có: tia CD nằm giữa hai tia CF và CB
=>\(\hat{BCF}=\hat{BCD}+\hat{FCD}=20^0+50^0=70^0\)
Ta có: \(\hat{BCF}=\hat{ABC}\left(=70^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CF
Ta có: \(\hat{EDC}+\hat{DCF}=130^0+50^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên ED//CF
Ta có: AB//CF
ED//CF
Do đó: AB//DE
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 9
Đặt \(A=1+\frac12+\frac{1}{2^2}+\cdots+\frac{1}{2^{2023}}+\frac{1}{2^{2024}}\)
\(2A=2+1+\frac12+\frac{1}{2^2}+\cdots+\frac{1}{2^{2022}}+\frac{1}{2^{2023}}\)
\(2A-A=2-\frac{1}{2^{2024}}\)
\(A=2-\frac{1}{2^{2024}}\)
Thay vào pt ban đầu:
\(\left(x+\frac12\right)^{2024}=2-\left(2-\frac{1}{2^{2024}}\right)\)
\(\left(x+\frac12\right)^{2024}=\frac{1}{2^{2024}}=\left(\frac12\right)^{2024}\)
\(x+\frac12=\frac12\) hoặc \(x+\frac12=-\frac12\)
\(x=0\) hoặc \(x=-1\)
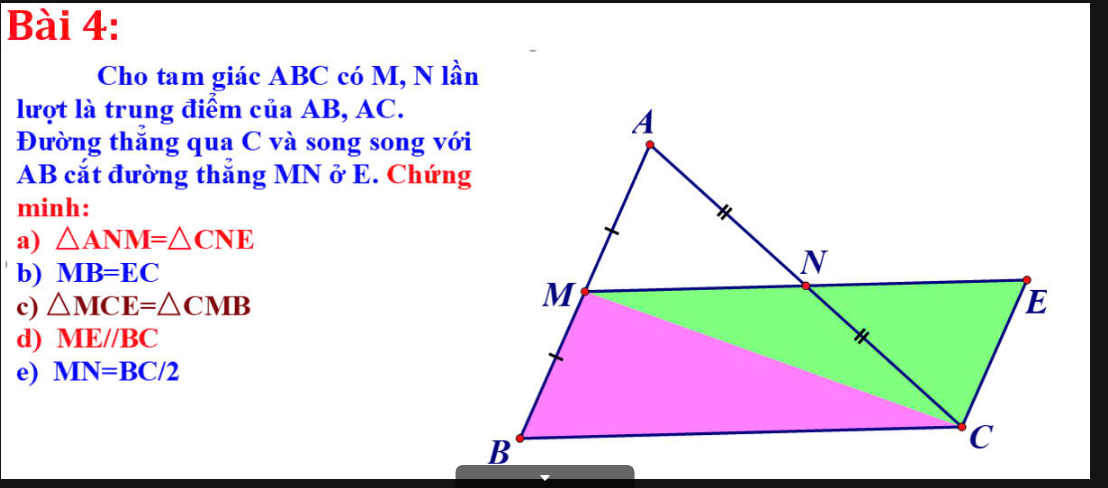
Giải:
a; Xét tam giác ANM và tam giác CNE có:
AN = NC (gt); góc ANM = góc CNE (đối đỉnh)
Góc MAN = góc NCE (so le trong)
Suy ra: Δ ANM = Δ CNE(g -c - g)
b; Δ ANM = Δ CNE (cmt)
Suy ra: MA = EC (hai cạnh tương ứng)
MA = MB (gt)
Suy ra: MB = EC (tính chất bắc cầu)
c; Xét Δ MCE và Δ CMB có:
MB = CE (cmt)
MC chung
Góc BMC = góc MCE (so le trong)
Suy ra Δ MCE = Δ CMB (c - g - c)
d; Xét tứ giác BCEM có:
MB = EC (cmt)
MB // EC (gt)
Suy ra tứ giác BCEM là hbh (tứ giác có một cặp cạnh đối diện song song và bẳng nhau tứ giác đó là hbh)
Suy ra ME // BC
e; Δ ANM = Δ CNE (cmt)
Suy ra: AM = CE
Mặt khác AM // CE (gt)
Suy ra tứ giác AECM là hbh(tứ giác có một cặp cạnh đối diện song song và bẳng nhau tứ giác đó là hbh)
Suy ra: MN = NE (hbh có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
MN = \(\frac12ME\)
Mà tứ giác BCEM là hbh (cmt)
Suy ra: BC = ME
Suy ra: MN = \(\frac12\) BC (đpcm)
BC (đpcm)a; Xét tam giác ANM và tam giác CNE có: AN = NC (gt); góc ANM = góc CNE (đối đỉnh) Góc MAN = góc NCE (so le trong) Suy ra: Δ ANM = Δ CNE(g -c - g) b; Δ ANM = Δ CNE (cmt) Suy ra: MA = EC (hai cạnh tương ứng) MA = MB (gt) Suy ra: MB = EC (tính chất bắc cầu) c; Xét Δ MCE và Δ CMB có: MB = CE (cmt) MC chung Góc BMC = góc MCE (so le trong) Suy ra Δ MCE = Δ CMB (c - g - c) d; Xét tứ giác BCEM có: MB = EC (cmt) MB // EC (gt) Suy ra tứ giác BCEM là hbh (tứ giác có một cặp cạnh đối diện song song và bẳng nhau tứ giác đó là hbh) Suy ra ME // BC ; Δ ANM = Δ CNE (cmt) Suy ra: AM = CE Mặt khác AM // CE (gt) Suy ra tứ giác AECM là hbh(tứ giác có một cặp cạnh đối diện song song và bẳng nhau tứ giác đó là hbh) Suy ra: MN = NE (hbh có hai đường chéo cắt nhau tại trung điểm của mỗi đường) MN = 1 2 M E 2 ME Mà tứ giác BCEM là hbh (cmt) Suy ra: BC = ME Suy ra: MN = 1/2