Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
 Ta có:
Ta có:
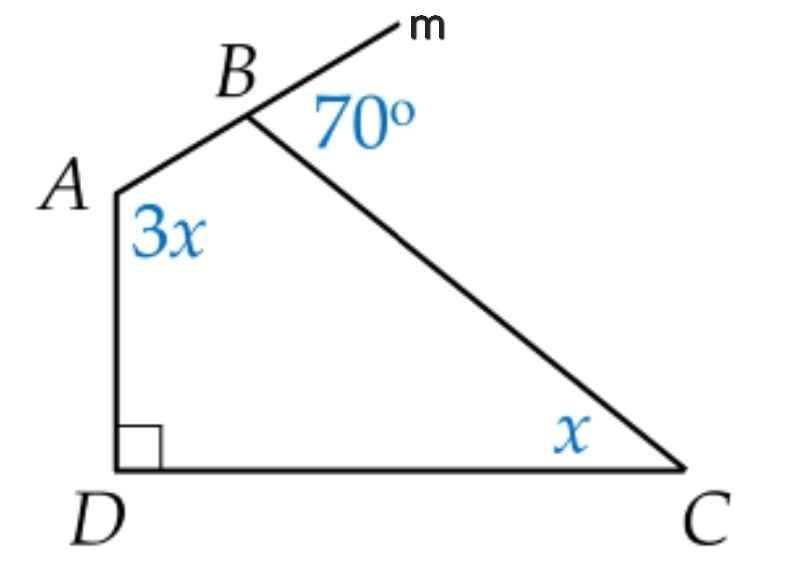
∠ABC + ∠CBm = 180⁰ (kề bù)
⇒ ∠ABC = 180⁰ - ∠CBm
= 180⁰ - 70⁰
= 110⁰
Tứ giác ABCD có:
∠A + ∠ABC + ∠C + ∠D = 360⁰ (tổng bốn góc trong tứ giác ABCD)
⇒ 3x + 110⁰ + x + 90⁰ = 360⁰
⇒ 4x + 200⁰ = 360⁰
⇒ 4x = 360⁰ - 200⁰
4x = 160⁰
⇒ x = 160⁰ : 4
⇒ x = 40⁰
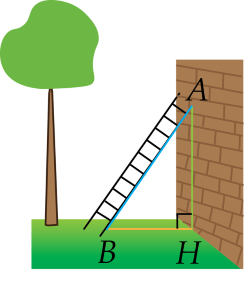
b) ∆ABH vuông tại H
⇒ AB² = AH² + BH² (Pytago)
⇒ AH² = AB² - BH²
= 3,7² - 1,2²
= 12,25
⇒ AH = 3,5
⇒ AH/BH = 3,5/1,2 ≈ 2,9 > 2,2
Vậy thang cách chân tường không "an toàn"
a) Góc ngoài tại đỉnh \(B\) có số đo bằng \(7 0^{\circ}\) nên góc trong tại đỉnh \(B\) có số đo bằng \(18 0^{\circ} - 7 0^{\circ} = 11 0^{\circ}\)
Xét tứ giác \(A B C D ,\) ta có: \(\hat{A} + \hat{B} + \hat{C} + \hat{D} = 36 0^{\circ}\)
Do đó \(3 x + 11 0^{\circ} + x + 9 0^{\circ} = 36 0^{\circ}\)
uy ra \(4 x = 16 0^{\circ}\) nên \(x = 4 0^{\circ}\)
Vậy \(x = 4 0^{\circ}\).
b) Áp dụng định lí Pythagore vào tam giác \(A B H\) vuông tại \(H\) ta có: \(A B^{2} = A H^{2} + B H^{2}\)
Suy ra \(A H^{2} = A B^{2} - B H^{2}\)
Do đó \(A H = \sqrt{A B^{2} - B H^{2}} = \sqrt{3 , 7^{2} - 1 , 2^{2}} = 3 , 5\) m
Ta có \(\frac{A H}{B H} = \frac{3 , 5}{1 , 2} \approx 2 , 9\)
Mà \(2 , 9 > 2 , 2\) nên khoảng cách đặt thang cách chân tường đã cho là không an toàn.

a) Xét tứ giác ABCD ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\Rightarrow\widehat{D}=360^o-102^o-102^o-102^o\)
\(\Rightarrow\widehat{D}=54^o\)
b) Xét tam giác vuông AOD ta có:
\(AD^2=OD^2+OA^2\)
\(\Rightarrow OA=\sqrt{AD^2-OD^2}\)
\(\Rightarrow OA=\sqrt{30^2-26,7^2}\approx13,7\left(cm\right)\)
Xét tam giác vuông AOB ta có:
\(AB^2=OA^2+OB^2\)
\(\Rightarrow OB=\sqrt{AB^2-OA^2}\)
\(\Rightarrow OB=\sqrt{17,5^2-13,7^2}\approx10,9\left(cm\right)\)
Độ dài đường chéo BD là:
\(BD=OB+OD=26,7+10,9\approx37,6\left(cm\right)\)
a) Số đo góc \(D\) ở đuôi chiếc diều là: \(\hat{D} = 36 0^{\circ} - \left(\right. \hat{A} + \hat{B} + \hat{C} \left.\right) = 36 0^{\circ} - \left(\right. 10 2^{\circ} + 10 2^{\circ} + 10 2^{\circ} \&\text{nbsp}; \left.\right) = 5 4^{\circ} .\)
b) Xét \(\Delta O A D\) vuông tại \(O\), theo định lí Pythagore ta có:
\(O A^{2} = A D^{2} - O D^{2} = 30^{2} - 26 , 7^{2} = 187 , 11\)
Xét \(\Delta O A B\) vuông tại \(O ,\) theo định lí Pythagore ta có:
\(O B^{2} = A B^{2} - O A^{2} = 17 , 5^{2} - 187 , 11 = 119 , 14\)
Do đó \(O B = \sqrt{119 , 14} \approx 10 , 9\) (cm).
Suy ra \(B D = O B + O D = 10 , 9 + 26 , 7 = 37 , 6\) (cm).

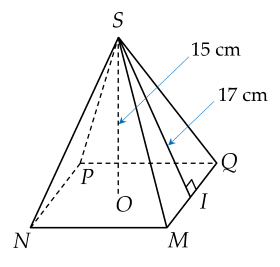
\(V_{S.MNPQ}=\dfrac{1}{3}.S_{MNPQ}.SO\)
\(\Rightarrow S_{MNPQ}=\dfrac{3.V_{S.MNPQ}}{SO}=\dfrac{3.1280}{15}=256cm^2\)
Xét tg vuông SOI
\(OI=\sqrt{SI^2-SO^2}\) (Pitago)
\(\Rightarrow OI=\sqrt{17^2-15^2}=8cm\)
Ta có
\(OI=\dfrac{MN}{2}\Rightarrow MN=2.OI=2.8=16cm\)
Ta có:
\(V=\dfrac{1}{3}.S_{MNPQ}.15=1280\left(cm^3\right)\)
\(\Rightarrow S_{MNPQ}=\dfrac{1280.3}{15}=256\left(cm^2\right)\)
\(\Rightarrow MN=\sqrt{256}=16\left(cm\right)\)

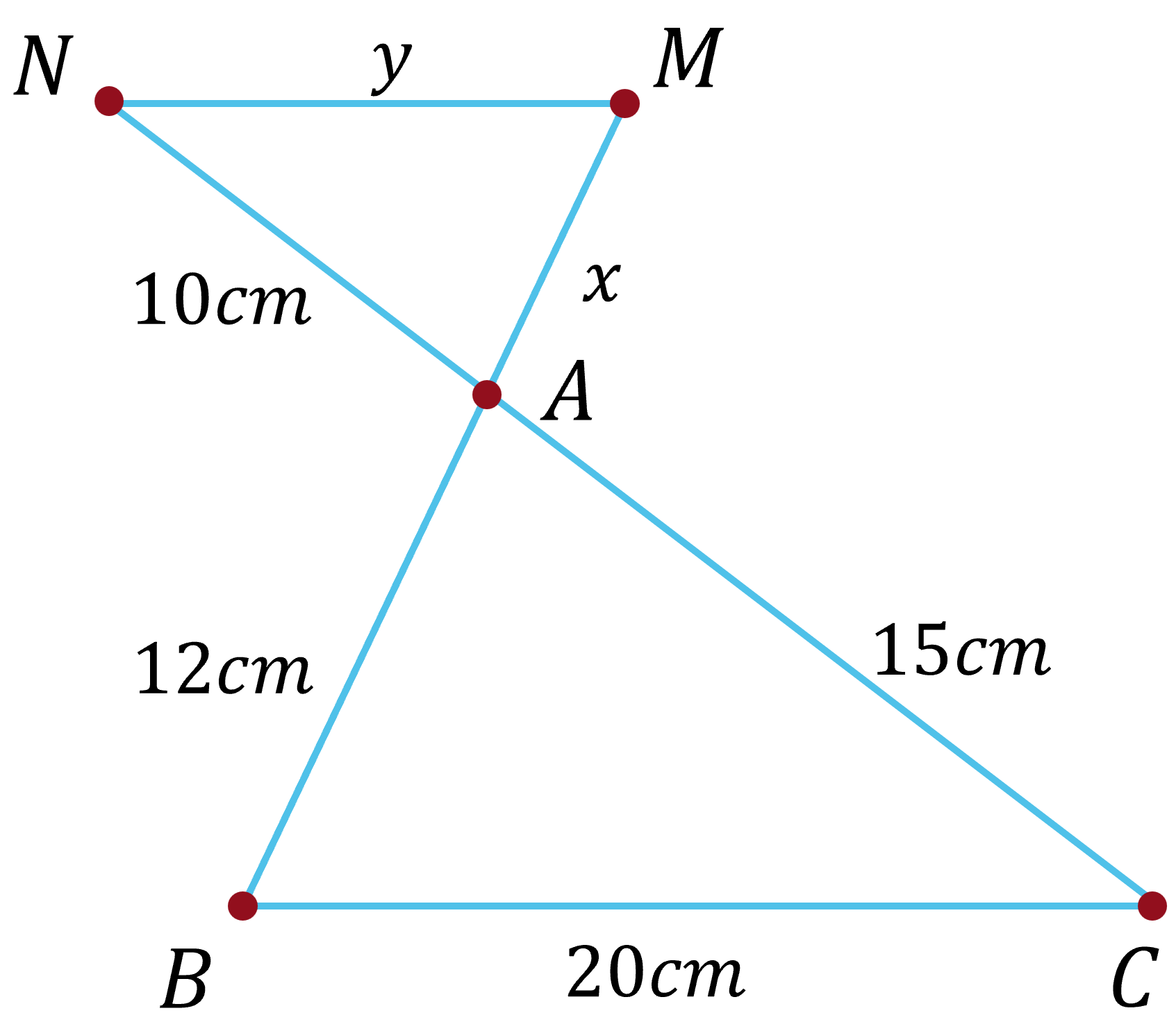
Vì MN // BC theo Talet ta có:
\(\dfrac{y}{20}\) = \(\dfrac{10}{15}\) = \(\dfrac{x}{12}\) => x = \(\dfrac{10}{15}\) . 12 = 8; y = \(\dfrac{10}{15}\) . 20 = \(\dfrac{40}{3}\)

\(C=\left(x^2-1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^4-1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^8-1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^{16}-1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^{32}-1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=x^{64}-1-x^{64}\)
\(C=-1\)
Vậy gtri của C không phụ thuộc vào x

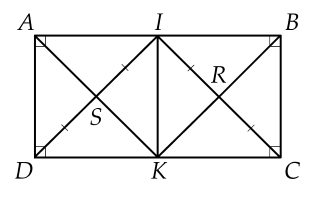
a) Vì ��=2��AB=2BC suy ra ��=��2=��BC= AB/2=AD
ABCD là hình chữ nhật nên AB=DC suy ra 1/2AB=1/2DC do đó AI=DK=AD
Tứ giác AIKD có AI//DK, AI=DK nên tứ giác AIKD là hình bình hành
Lại có AD=AI nên AIKD là hình thoi
Mà góc IAD= 90 độ do đó AIKD là hình vuông
Vậy tứ giác AIKD là hình vuông
Chứng minh tương tự cho tứ giác BIKC
Vậy tứ gáic BIKC là hình vuông
b) VÌ AIKD là hình vuông nên DI là tia phân giác góc ADK nên góc IDK = 45 độ
Tương tự góc ICK = 45 độ
Tam giác IDC cân có góc DIC = 90 độ nên là tam gaic vuông cân
Vậy tam giác IDC là tam gáic vuông cân
c) Vì AIKD, BCKI là các hình vuông nên hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường nên SI=SK=DI/2 và IR=RK=IC/2
=>ISKR là hình thoi
Lại có góc DIC= 90 độ nên ISKR là hình vuông
Vậy ISKR là hình vuông

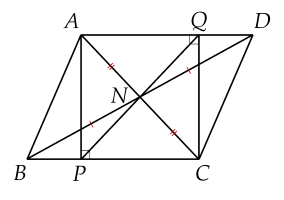
a) ����ABCD là hình bình hành.
b) �,�,�P,N,Q thẳng hàng.
c) Δ���ΔABC cần thêm điều kiện gì để tứ giác ����ABCD là hình vuông.
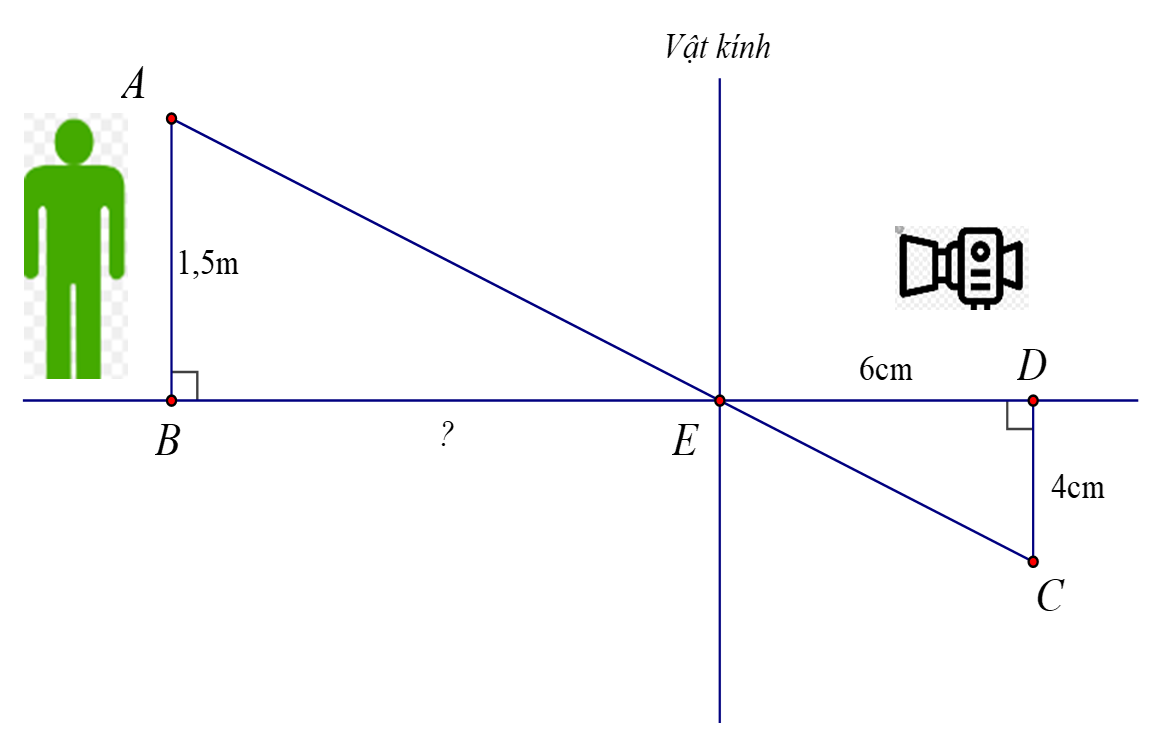





Do AB//CD( vì cùng vuông góc với BD)
Nên áp dụng định lí Ta lét , ta được :
EB/ED=AB/CD
=> EB/6 = 150/4
=> EB = 150.6/4 = 225 (cm)
Đổi đơn vị: 1,51,5 m =150=150 cm.
Ta có ��AB // ��CD (cùng vuông góc ��BD) suy ra ����=����EDEB=DCAB (định lí Thalès)
Suy ra ��=��.����=150.64=225EB=DCAB.ED=4150.6=225 (cm).
Vậy người đứng cách vật kính máy ảnh là 225225 cm.