
a) Ta thấy ngay tam giác MAE và tam giác MEC có chung chiều cao hạ từ M xuống AC, EC = 4AE nên \(S_{MEC}=4S_{MAE}=4\times20=80\left(cm^2\right)\)
b) Ta thấy tam giác MBD và tam giác MCD có chung chiều cao và đáy BD = DC nên \(S_{MBD}=S_{MCD}\)
Ta thấy tam giác EBD và tam giác ECD có chung chiều cao và đáy BD = DC nên \(S_{EBD}=S_{ECD}\)
Vậy nên \(S_{MBE}=S_{MEC}=80\left(cm^2\right)\)
Ta có \(\frac{S_{AME}}{S_{MEC}}=\frac{1}{4};\frac{S_{ABE}}{S_{EBC}}=\frac{1}{4}\Rightarrow\frac{S_{AME}+S_{ABE}}{S_{MEC}+S_{EBC}}=\frac{1}{4}\Rightarrow\frac{S_{MBE}}{S_{MEBC}}=\frac{1}{4}\)
\(\Rightarrow S_{MEBC}=4.80=320\left(cm^2\right)\)
\(\Rightarrow S_{MBC}=320+80=400\left(cm^2\right)\)
\(\Rightarrow S_{ABC}=400-20-80=300\left(cm^2\right)\)

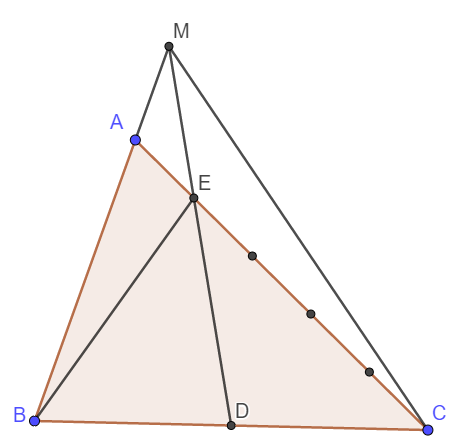
Cho tam giác ABC. Gọi D là điểm chính giữa của cạnh BC. Lấy E trên cạnh AC sao cho AE bằng 1/5 AC. Nối D với E. Kéo dài DE cắt AB kéo dài tại M. Nối M với C. Biết diện tích AME bằng 20 cm2 .Tính diện tích MEC và ABC?
Được cập nhật 22 tháng 5 2019 lúc 20:10
4
![]()
![]()
Hoàng Thị Thu Huyền Quản lý
7 tháng 3 2018 lúc 10:05

a) Ta thấy ngay tam giác MAE và tam giác MEC có chung chiều cao hạ từ M xuống AC, EC = 4AE nên SMEC=4SMAE=4×20=80(cm2)
b) Ta thấy tam giác MBD và tam giác MCD có chung chiều cao và đáy BD = DC nên SMBD=SMCD
Ta thấy tam giác EBD và tam giác ECD có chung chiều cao và đáy BD = DC nên SEBD=SECD
Vậy nên SMBE=SMEC=80(cm2)
a, AC = AE + EC; AE = EC \(\times\) 2 ⇒ EC = \(\dfrac{AE}{2}\)
Thay EC = \(\dfrac{AE}{2}\) vào biểu thức: AC = AE + EC ta được:
AC = AE + \(\dfrac{AE}{2}\) = AE \(\times\) \(\dfrac{3}{2}\)
Tỉ số cạnh AE và AC là: 1 : \(\dfrac{3}{2}\) = \(\dfrac{2}{3}\)
SAED = SACD \(\times\) \(\dfrac{2}{3}\) ( vì hai tam giác có chung đường cao hạ từ đỉnh D xuống cạnh AC và tỉ số cạnh đáy là \(\dfrac{2}{3}\))
Vì D điểm chính giữa của AB nên: AD = \(\dfrac{1}{2}\) AC
SACD = SABC \(\times\) \(\dfrac{1}{2}\) (vì hai tam giác có chung đường cao hạ từ đỉnh C xuống đáy AB và tỉ số hai cạnh đáy là \(\dfrac{1}{2}\))
Thay SACD = SABC \(\times\) \(\dfrac{1}{2}\) vào biểu thức SAED = SACD \(\times\) \(\dfrac{2}{3}\) ta có:
SAED = SABC \(\times\) \(\dfrac{1}{2}\) \(\times\) \(\dfrac{2}{3}\) = SABC \(\times\) \(\dfrac{1}{3}\)
SAED = 240 \(\times\) \(\dfrac{1}{3}\) = 80 (m2)
b, SBDM = SADM ( vì hai tam giác có chung đường cao hạ từ đỉnh M xuống cạnh đáy AB và AD = BD)
SBDM = SBCED + SCEM = SABC - SAED + SCEM
SBDM = 240 - 80 + SCEM = 160 + SCEM
SADM = SADE + SAEM = 80 + SAEM
⇒ 160 +SCEM = 80 + SAEM
⇒ SCEM + 80 = SAEM
\(\) SAEM = SCEM \(\times\) 2( vì hai tam giác có chung chiều cao hạ từ đỉnh M xuống đáy AC và AE = CE \(\times\) 2)
Ta có sơ đồ:
Theo sơ đồ ta có: SCEM = 80 : ( 2-1) = 80 (m2)
CE = AC - AE = AC - CE \(\times\) 2 ⇒ CE + CE \(\times\) 2 = AC
⇒ CE \(\times\) 3 = AC
SABC = SBCE \(\times\) 3 (Vì hai tam giác có chung đường cao hạ từ đỉnh B xuống đáy AC và AC = CE \(\times\) 3)
⇒ SBCE = 240 : 3 = 80 (m2)
Do tam giác CEM và tam giác BCE có chung đường cao hạ từ đỉnh E xuống đáy BC nên chiều cao của tam giác CEM hạ từ đỉnh E xống đáy CM bằng:
80 \(\times\) 2 : 24 = \(\dfrac{20}{3}\) (m)
Độ dài đáy CM là: 80 \(\times\) 2 : \(\dfrac{20}{3}\) = 24 (m)
Đáp số: a, 80 m2
b, 24 m
a) Ta thấy ngay tam giác MAE và tam giác MEC có chung chiều cao hạ từ M xuống AC, EC = 4AE nên ����=4����=4×20=80(��2)SMEC=4SMAE=4×20=80(cm2)
b) Ta thấy tam giác MBD và tam giác MCD có chung chiều cao và đáy BD = DC nên ����=����SMBD=SMCD
Ta thấy tam giác EBD và tam giác ECD có chung chiều cao và đáy BD = DC nên ����=����SEBD=SECD
Vậy nên ����=����=80(��2)SMBE=SMEC=80(cm2)
Ta có ��������=14;��������=14⇒����+��������+����=14⇒���������=14SMECSAME=41;S
Đúng(0)