Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

O x y t H A B C
a) Xét2 \(\Delta vuông\)AHO va BHO co
góc AOH = góc BOH ( Ot là tia phân giác góc xOy)
OH là cạnh chung
\(\Rightarrow\Delta AHO=\Delta BHO\)(góc vuông,góc nhọn kề cạnh ấy)
\(\Rightarrow OA=OB\)(2 cạnh tương ứng)
b) Xét \(\Delta OAC\)và \(\Delta OBC\)có:;
OA = OB ( chứng minh trên)
góc AOH = góc BOH ( giả thiết )
OC là cạnh chung
\(\Rightarrow\Delta OAC=\Delta OBC\)(c.g.c)
\(\Rightarrow CA=CB\)( 2 cạnh tương ứng)
và góc OAC = góc OBC ( 2 góc tương ứng)

+) Xét tg ONB và OMA có
OB= OA (gt)
Góc O chung
Góc B = góc A(=90)
=> ∆ OMA (ch - gn)
=> />+) Ta có OA + AN = ON
OB+ BM= OM
Mà OA= OB
/>=> AN = BM
+) XÉT ∆OAH và ∆ OBH
OH cạnh cchung
OA= OB
góc A = góc B
=>∆ OAH= ∆ OBH( cho CGV)
=> AOH= BOH
=> OH là phân giác xOy
ta có (cmt)
=> ∆ ONM cân tại O
OI là trung tuyến => OI là đường cao
OI vuông góc NM(1)
Ta có MA, NB lần lượt vuông góc với Ox, Oy
MA cắt NB tại H
=> H là trực tâm của ∆OMN
=> OH vuông góc NM(2)
từ (1)(2)=> O , H , I thẳng hàng ( qua O chỉ kẻ đc duy nhất 1 đường thẳng vuông góc NM)

a) Ta có: OC=OA+AC
OD=OB+BD
Mà OA=OB và AC=BD (gt)
=>OC=OD
Xét Δ OAD và Δ OBC có:
OA=OB (gt)
ˆOO^ góc chung
OC=OD (cmt)
=> Δ OAD=Δ OBC (c.g.c)
=> AD=BC (2 cạnh tương ứng)
Δ OAD=Δ OBC (cmt)
=> ˆD=ˆCD^=C^ và ˆA1=ˆB1A1^=B1^ (2 góc tương ứng)
Mà ˆA1+ˆA2=ˆB1+ˆB2A1^+A2^=B1^+B2^= 1800 (kề bù)
=> ˆA2=ˆB2A2^=B2^
Δ EAC và Δ EBD có:
ˆC=ˆDC^=D^ (cmt)
AC=BD (gt)
ˆA2=ˆB2A2^=B2^ (cmt)
=> Δ EAC= ΔEBD (g.c.g)
c) Δ EAC=ΔEBD (cmt)
=> EA=EB (2 cạnh tương ứng)
ΔOBE và Δ OAE có:
OB=OA (gt)
ˆB1=ˆA1B1^=A1^ (cmt)
EA=EB (cmt)
=>Δ OBE=Δ OAE (c.g.c)
=> ˆO1=ˆO2O1^=O2^ (2 góc tương ứng)
Vậy OE là phân giác ˆxO
Phân tích bài toán
- Đề bài cho:
- Góc nhọn xOy
- Điểm A thuộc Ox, điểm B thuộc Oy, OA = OB
- Điểm C thuộc tia Ax, điểm D thuộc tia By, AC = BD
- Yêu cầu:
- Chứng minh AD = BC
- Chứng minh △EAC = △EBD (với E là giao điểm của AD và BC)
- Chứng minh OE là phân giác góc xOy
a. Chứng minh AD = BC
Xét △OAD và △OBC, ta có:
- OA = OB (giả thiết)
- ∠xOy chung
- OD = OB + BD
- OC = OA + AC
Vì OA = OB và AC = BD nên OA + AC = OB + BD, suy ra OC = OD.
Vậy, △OAD = △OBC (c.g.c). Suy ra, AD = BC (hai cạnh tương ứng).
b. Chứng minh △EAC = △EBD
Xét △OAD = △OBC (chứng minh trên), suy ra:
- ∠OAD = ∠OBC
- ∠ODA = ∠OCB
Ta có:
- ∠EAC = 180° - ∠OAD
- ∠EBD = 180° - ∠OBC
Vì ∠OAD = ∠OBC nên ∠EAC = ∠EBD.
Xét △EAC và △EBD, ta có:
- ∠EAC = ∠EBD (chứng minh trên)
- AC = BD (giả thiết)
- ∠ACE = 180° - ∠OCB
- ∠BDE = 180° - ∠ODA
Vì ∠OCB = ∠ODA nên ∠ACE = ∠BDE.
Vậy, △EAC = △EBD (g.c.g).
c. Chứng minh OE là phân giác góc xOy
Xét △OAE và △OBE, ta có:
- OA = OB (giả thiết)
- OE là cạnh chung
Từ △EAC = △EBD (chứng minh trên), suy ra AE = BE (hai cạnh tương ứng).
Vậy, △OAE = △OBE (c.c.c). Suy ra, ∠AOE = ∠BOE (hai góc tương ứng).
Do đó, OE là tia phân giác của góc xOy.
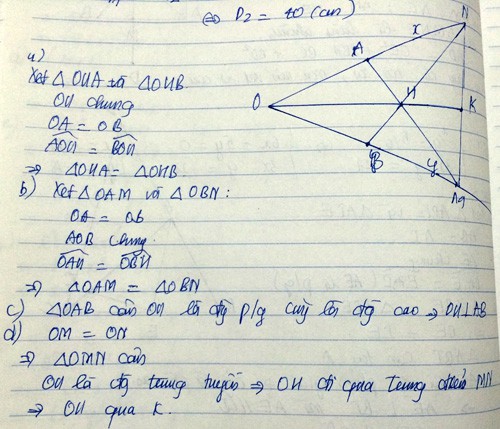
a: Xét ΔOAM vuông tại A và ΔOBN vuông tại B có
OA=OB
góc O chung
Do đo: ΔOAM=ΔOBN
=>OM=ON
OA+AN=ON
OB+BM=Om
mà OA=OB;ON=OM
nên AN=BM
b: Xét ΔOAH vuông tại A va ΔOBH vuông tại B có
OH chung
OA=OB
Do đó: ΔOHA=ΔOHB
=>góc AOH=góc BOH
=>OH là phân giác của góc xOy
Xét ΔHAN vuông tại A va ΔHBM vuông tại B co
HA=HB
góc AHN=góc BHM
DO đó: ΔHAN=ΔHBM
=>HN=HM
mà ON=OM
nên OH là đường trung trực của MN
mà I nằm trên đường trung trực của MN
nên O,H,I thẳng hàng
ngốn ah