Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn 1 điểm bất kì, từ điểm đó kẻ tới n-1 điểm con lại ta được n-1 đường mà có n điểm => có n.(n-1) đường nhưng như vậy số đường thẳng đã được tính 2 lần nên số đường thẳng thực tế là: n.(n-1):2 (đường)
Ta có: n.(n-1):2 = 28
=> n.(n-1) = 28.2
=> n.(n-1) = 56 =8.7
=> n = 8
Vậy n = 8
Công thức tính điểm pít số đường thẳng cho trc học ở lớp 6 là n.(n + 1) / 2
Theo bài ra ta có: n.(n + 1) / 2 = 28
=> n.(n + 1) = 56
=> n.(n + 1) = 7.8
=> n = 7
Vậy n = 7

Theo đề bài ta có:
\(\frac{n\left(n+1\right)}{2}=28\)
\(\Rightarrow n\left(n+1\right)=28.2=56\)
\(\Rightarrow n\left(n+1\right)=7.8\)
\(\Rightarrow n=7\)
Cứ n đường thẳng thì lại có thể nối với n - 1 điểm còn lại n - 1 và tạo thành n - 1 đương thẳng
Vậy có tất cả :\(\frac{\left(n-1\right)n}{2}\)
\(\Rightarrow\frac{\left(n-1\right)n}{2}=28\)
\(\Rightarrow n\left(n-1\right)=56\)
\(\Rightarrow n\left(n-1\right)=7.8\)
=> n = 7
Vậy có 7 đường thẳng

bài 1:Qua điểm A và mỗi điểm B,C,D có ba đường thằng là AB, AC,AD. Qua điểm B và mỗi điểm C,D có hai đường thẳng là BC,BD (Không qua A). Qua điểm C và D còn lại có một đường thẳng CD (không đi qua A,B).
Chú ý: có thể trình bày ngắn gọn như sau : với 4 điểm A,B,C,D thì có 6 đường thẳng AB,AC,AD,BC,BD,CD
bài 2:Vì 3 điểm M,N,P thẳng hàng nên đường thẳng đi qua cả 3 điểm M,N,P trùng nhau và Q nằm ngoài đường thẳng trên nên kẻ được 3 đường thẳng lần lượt đi qua 3 điểm thẳng hàng.
Vậy ta có 4 đường thẳng: MP,QN,QM,QP(không kể MN, NP)

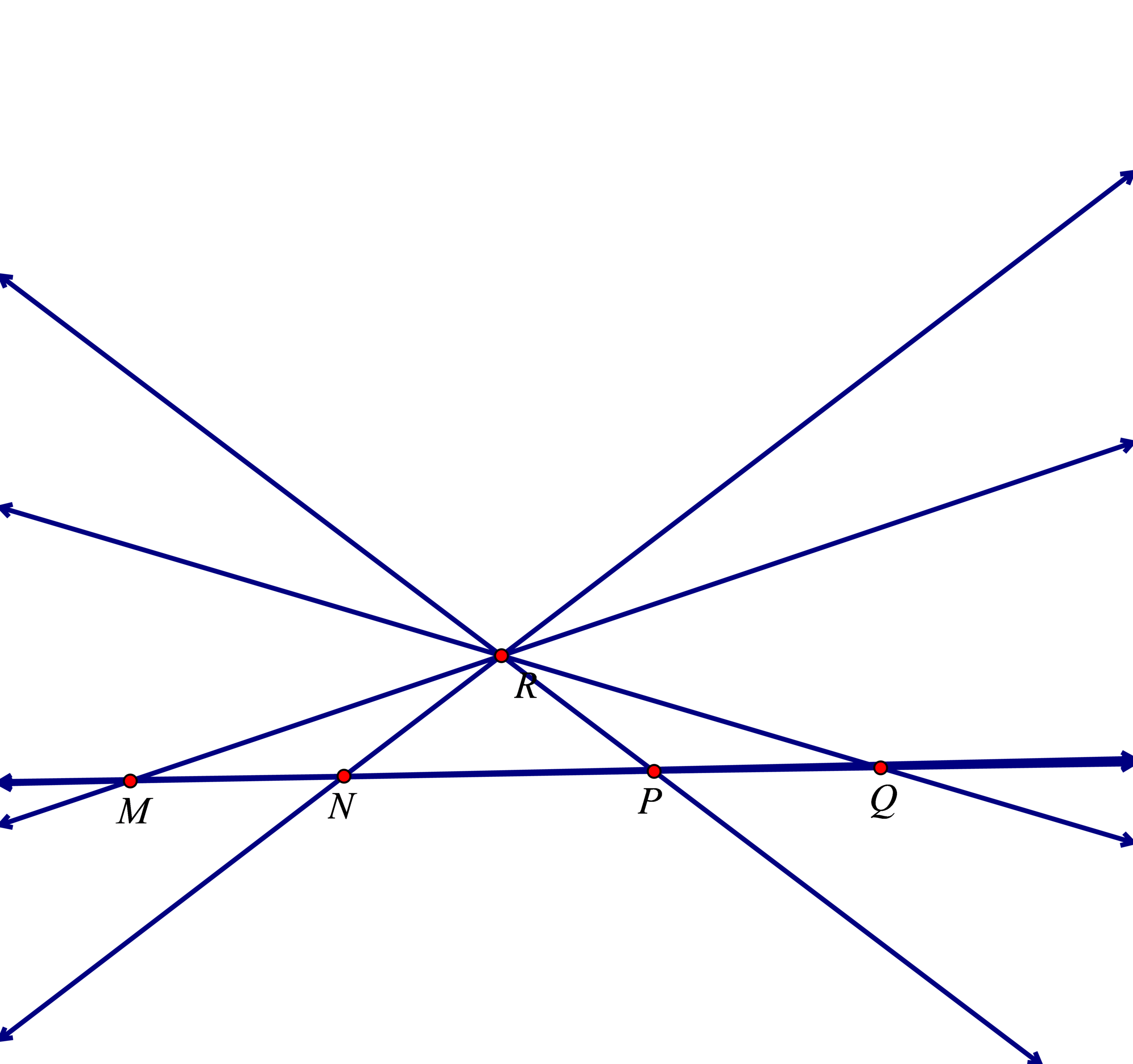
a) Có 5 đường thẳng, đó là đường thẳng MQ, RM, RN, RP, RQ.
b) Các tia gốc P là: PM, PN, PQ, PR. Hai tia PM, PN trùng nhau. Hai tia PM, PQ đối nhau.