Hàm số nào sau đây có đồ thị là parabol có đỉnh $I\left( -1;3 \right)$?

Bảng biến thiên của hàm số $y=-x^2+2x-1$ là

Hàm số $y=4x^2+8x-5$

Biết rằng $\left( P \right):y=a{{x}^{2}}-4x+c$ ($a \ne 0$) có hoành độ đỉnh bằng $-3$ và đi qua điểm $M\left( -2;1 \right)$. Tổng $S=a+c$ bằng

Hàm số nào sau đây đạt giá trị nhỏ nhất tại $x=\dfrac{3}{4}?$

Parabol $\left( P \right):y={{x}^{2}}+4x+4$ có số điểm chung với trục hoành là

Để $y = f(x) = (m-1) x^3 + 6mx^2 - 8$ là hàm số bậc hai thì điều kiện của tham số $m$ là

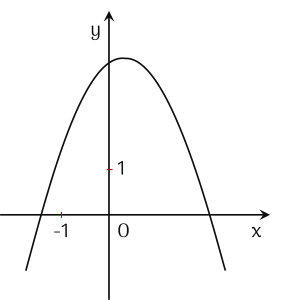
Hình trên là đồ thị của hàm số nào sau đây?

Hàm số nào sau đây nghịch biến trên khoảng $\left( -1;+\infty \right)$?

Giá trị lớn nhất của hàm số $y=-\sqrt{2}{{x}^{2}}+4x$ là

Gọi $S$ là tập hợp các giá trị thực của tham số $m$ sao cho parabol $\left( P \right):y={{x}^{2}}-4x+m$ cắt $Ox$ tại hai điểm phân biệt $A$; $B$ thỏa mãn $OA=3OB.$ Tổng các phần tử của $S$ là

Giá trị thực của $m$ để phương trình $\left| 2{{x}^{2}}-3x+2 \right|=5m-8x-2{{x}^{2}}$ có nghiệm duy nhất là

Hình nào sau đây là đồ thị hàm số $y = -4x|x|$?

Gọi $S$ là tập hợp tất cả các giá trị của tham số $m$ để hàm số $y=x^2+(m-1) x+2 m-1$ đồng biến trên khoảng $(-2 ;+\infty)$. Khi đó tập hợp $(-10 ; 10) \cap S$ là tập

Biết rằng hàm số $y=a{{x}^{2}}+bx+c\text{ }\left( a\ne 0 \right)$ đạt giá trị lớn nhất bằng $\dfrac{1}{4}$ tại $x=\dfrac{3}{2}$ và tổng lập phương các nghiệm của phương trình $y=0$ bằng $9.$ Tích $abc$ bằng

Cô Anh có $60$ m lưới muốn rào một mảnh vườn hình chữ nhật để trồng rau, biết rằng một cạnh là tường, cô Anh chỉ cần rào ba cạnh còn lại của hình chữ nhật để làm vườn. Diện tích lớn nhất mà cô Anh có thể rào được là

Cho parabol $\left( P \right):y={{x}^{2}}-4x+3$ và đường thẳng $d:y=mx+3$. Tất cả các giá trị thực của $m$ để $d$ cắt $\left( P \right)$ tại hai điểm phân biệt $A$ và $B$ sao cho diện tích tam giác $OAB$ bằng $\dfrac{9}{2}$ là