Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Tính đơn điệu; GTLN, GTNN của hàm số (tỉ lệ điểm mỗi dạng thức 4 : 3 : 3) SVIP

Cho hàm số y=f(x) có đồ thị như hình vẽ.
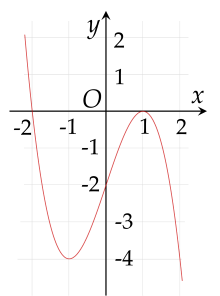
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Hàm số y=x3−3x2 nghịch biến trên khoảng nào dưới đây?
Cho hàm số y=x4+4x2+2. Mệnh đề nào dưới đây đúng?
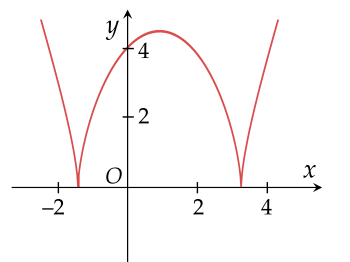
Cho hàm số y=f(x)=x2−2x−4 có đồ thị như hình vẽ. Hàm số y=f(x) có bao nhiêu điểm cực trị?
Cho hàm số y=f(x) có bảng biến thiên như sau:

Khẳng định nào sau đây đúng?
Giá trị lớn nhất của hàm số y=x−33x−1 trên đoạn [0;2] bằng
Cho hàm số y=f(x) xác định trên R và có đồ thị hàm số y=f′(x) là đường cong như hình vẽ dưới đây.
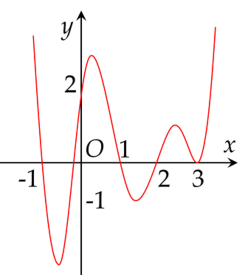
Hàm số y=f(x) có bao nhiêu điểm cực trị?
Giá trị lớn nhất và nhỏ nhất của hàm số y=2x3+3x2−1 trên đoạn [−2;1] lần lượt là
Cho hàm số y=f(x)=x−1x+1.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hàm số đã cho xác định trên R. |
|
| b) f′(x)=−(x−1)22. |
|
| c) Hàm số y=f(x) nghịch biến trên khoảng (−∞;1). |
|
| d) Hàm số y=f(x) không có cực trị. |
|
Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên:
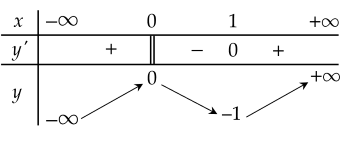
| a) Hàm số có giá trị cực tiểu bằng 1. |
|
| b) Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng −1. |
|
| c) Hàm số đạt cực đại tại x=0 và đạt cực tiểu tại x=1. |
|
| d) Hàm số có đúng một cực trị. |
|
Cho hàm số y=f(x) có đạo hàm f′(x)=(x+2)x(x−2) với mọi x∈R.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hàm số y=f(x) nghịch biến trên khoảng (0;2). |
|
| b) Hàm số y=f(x) đồng biến trên khoảng (−2;0). |
|
| c) Hàm số y=f(x) có hai điểm cực trị. |
|
| d) Hàm số y=f(x) có hai điểm cực tiểu. |
|
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc [−2025;2025] để hàm số y=ln(x2+2024)−mx+2025 đồng biến trên R?
Trả lời:
Có bao nhiêu giá trị của tham số m để đồ thị hàm số y=f(x)=31x3−21mx2+x−2 có giá trị tuyệt đối của hoành độ hai điểm cực trị là độ dài hai cạnh của tam giác vuông có cạnh huyền là 14?
Trả lời:
Độ cao so với mặt đất của một quả bóng được ném lên theo phương thẳng đứng được mô tả bởi hàm số bậc hai h(t)=−4,9t2+20t+1, trong đó độ cao h(t) tính bằng mét và thời gian t tính bằng giây. Tại thời điểm x giây kể từ khi bắt đầu được ném lên thì quả bóng đạt độ cao lớn nhất. Tính x. (kết quả làm tròn đến hàng phần trăm)
Trả lời:
