Mặt phẳng tọa độ và đồ thị hàm số SVIP

1. MẶT PHẲNG TỌA ĐỘ

MẶT PHẲNG TỌA ĐỘ

Trên mặt phẳng, ta vẽ hai trục số $Ox$, $Oy$ vuông góc với nhau và cắt nhau tại gốc $O$ của mỗi trục số như hình vẽ.

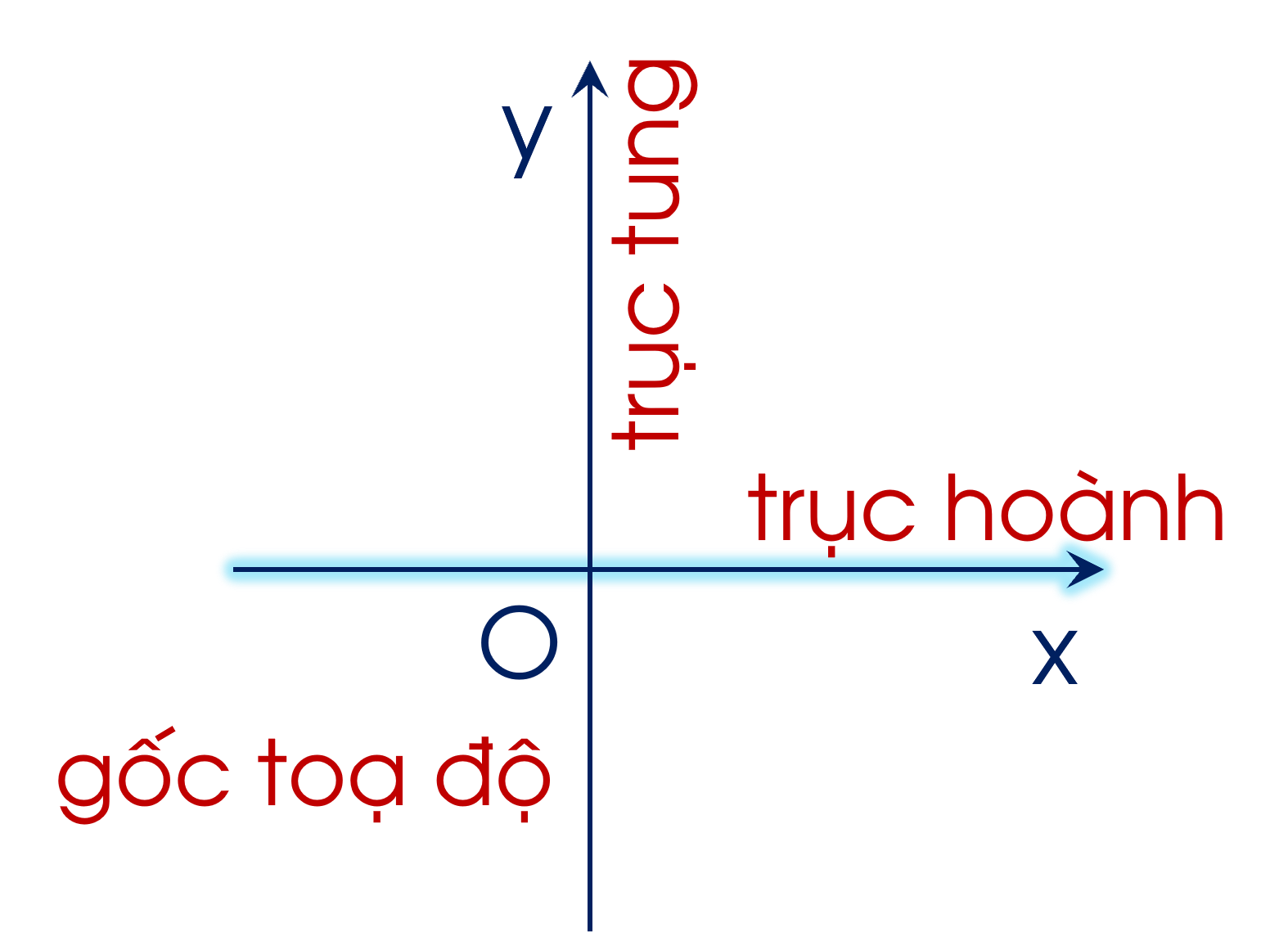
 + Các trục $Ox$ và $Oy$ gọi là các trục toạ độ, $Ox$ thường vẽ nằm ngang và gọi là trục hoành, $Oy$ thường vẽ thẳng đứng và gọi là trục tung.

+ Giao điểm $O$ gọi là gốc toạ độ.

+ Mặt phẳng có hệ trục toạ độ $Oxy$ gọi là mặt phẳng toạ độ.

TỌA ĐỘ ĐIỂM TRONG MẶT PHẲNG TỌA ĐỘ

Trong mặt phẳng toạ độ, mỗi điểm $M$ xác định duy nhất một cặp số $(x_0 ; y_0)$ và mỗi cặp số $(x_0 ; y_0)$ xác định duy nhất một điểm $M$.

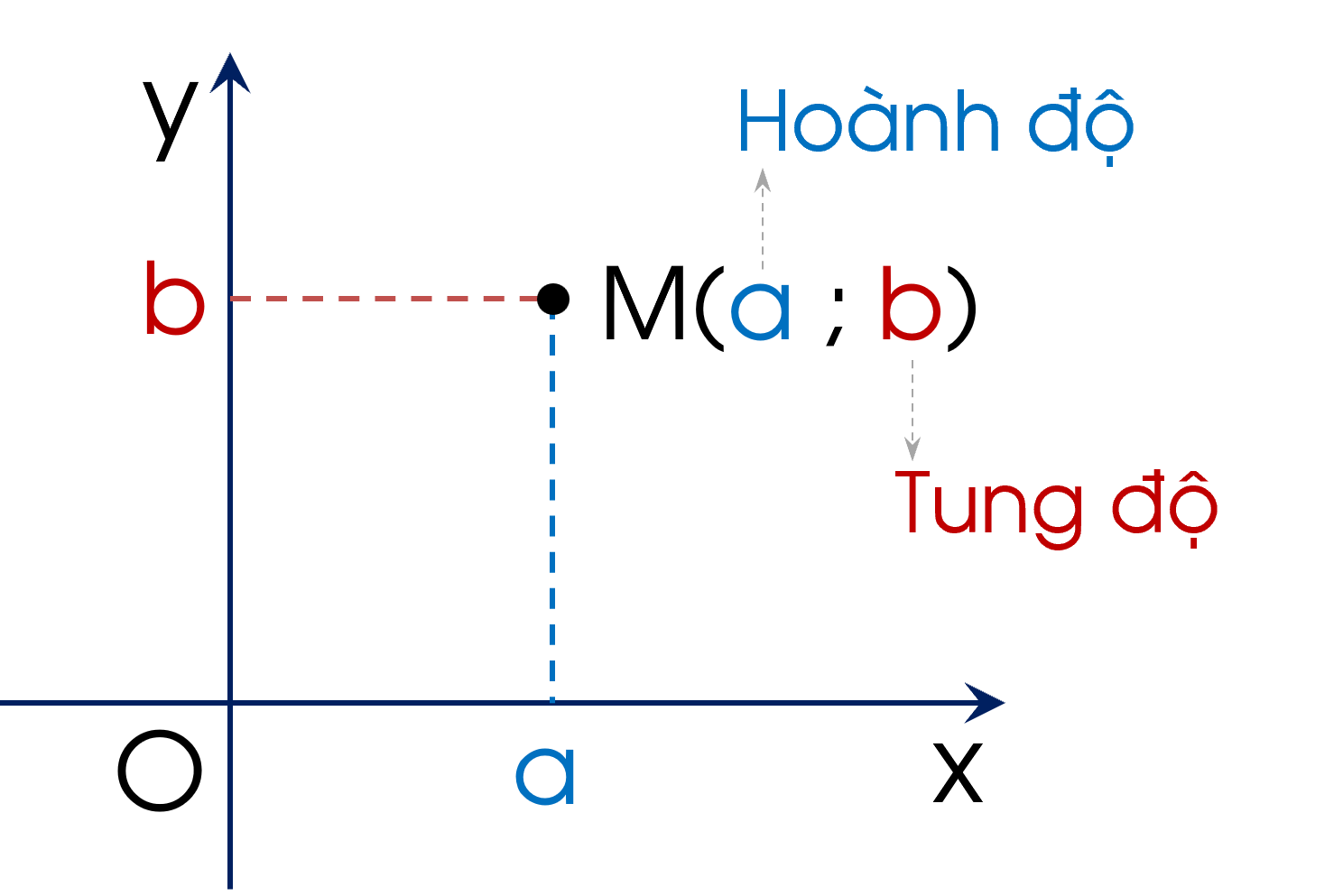
+ Cặp số $(x_0 ; y_0)$ là tọa độ điểm $M$; kí hiệu $M(x_0 ; y_0)$. Trong đó, $x_0$: hoành độ của điểm $M$; $y_0$: tung độ của điểm $M$.

+ Các đơn vị dài trên hai trục tọa độ thường được chọn bằng nhau (nếu không nói gì thêm).

Ví dụ 1. Dựa vào hình dưới và

a) Viết tọa độ điểm $A$, $B$.

b) Xác định các điểm $C(-2;1)$ và $D(0; -2)$ trong hình.

Lời giải

a) Ta có tọa độ hai điểm $A$, $B$ là: $A(2;2)$; $B(-1;0)$.

b) Các điểm $C(-2;1)$ và $D(0; -2)$ được xác định như sau:

Chú ý.

+ Hệ trục toạ độ $Oxy$ chia mặt phẳng toạ độ thành 4 góc phần tư (góc phần tư thứ I, II, III, IV).

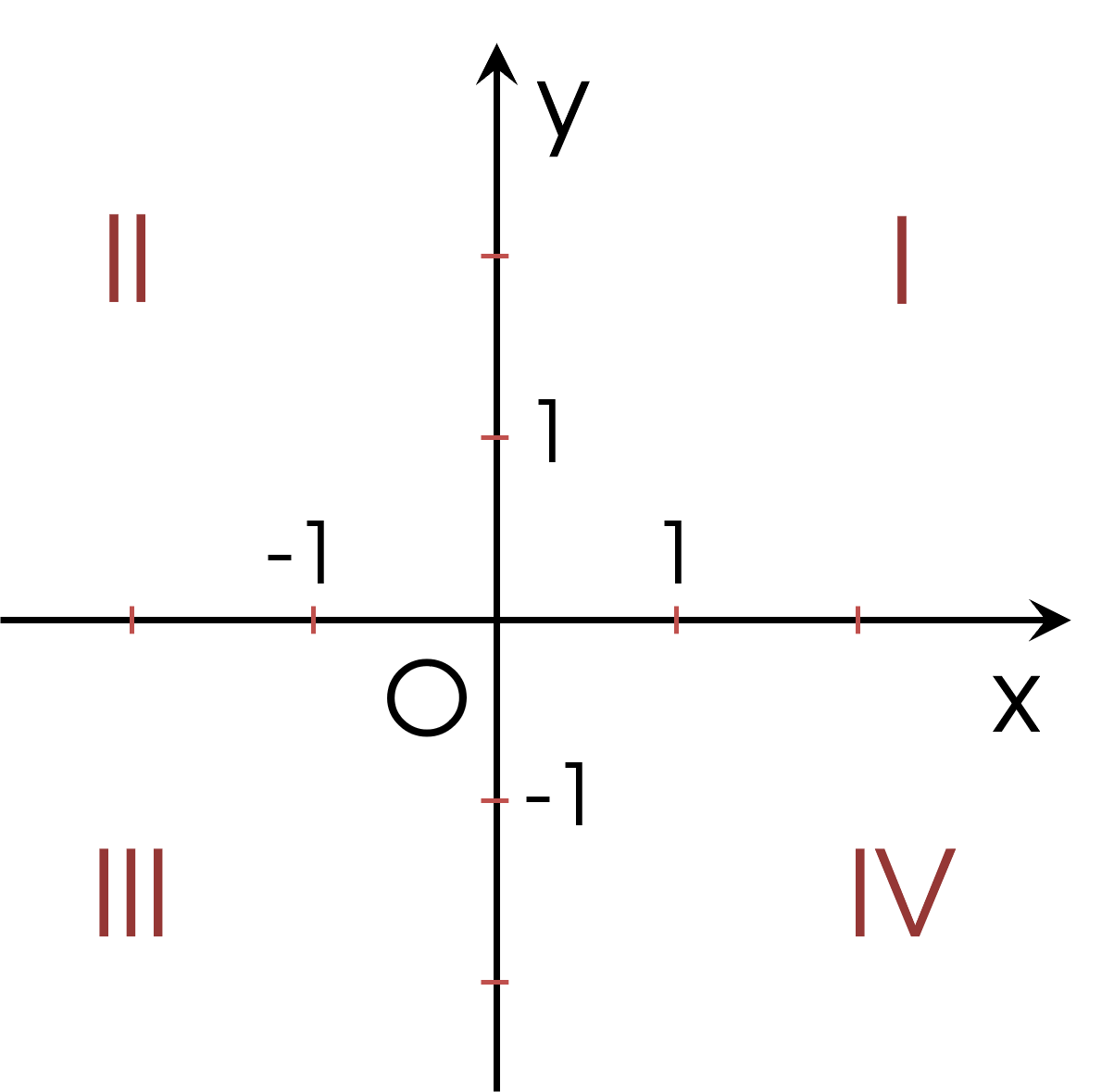
 + Các điểm có hoành độ (hoặc tung độ) bằng $0$ nằm trên trục tung $Oy$ (hoặc trục hoành $Ox$).

Ví dụ 2. $M(0 ; b)$ thuộc $Oy$; $N(a ; 0)$ thuộc $Ox$.

2. ĐỒ THỊ HÀM SỐ

Định nghĩa

Đồ thị của hàm số $y = f(x)$ là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng $(x ; y)$ trên mặt phẳng toạ độ.

Ví dụ 3. Vẽ đồ thị của hàm số $y = f(x)$ cho bởi bảng:

Lời giải

Đồ thị hàm số $y = f(x)$ gồm $4$ điểm như hình vẽ trên.

Ví dụ 4. Trong mặt phẳng tọa độ $Oxy$, cho đồ thị của hàm số $y = x + 2$.

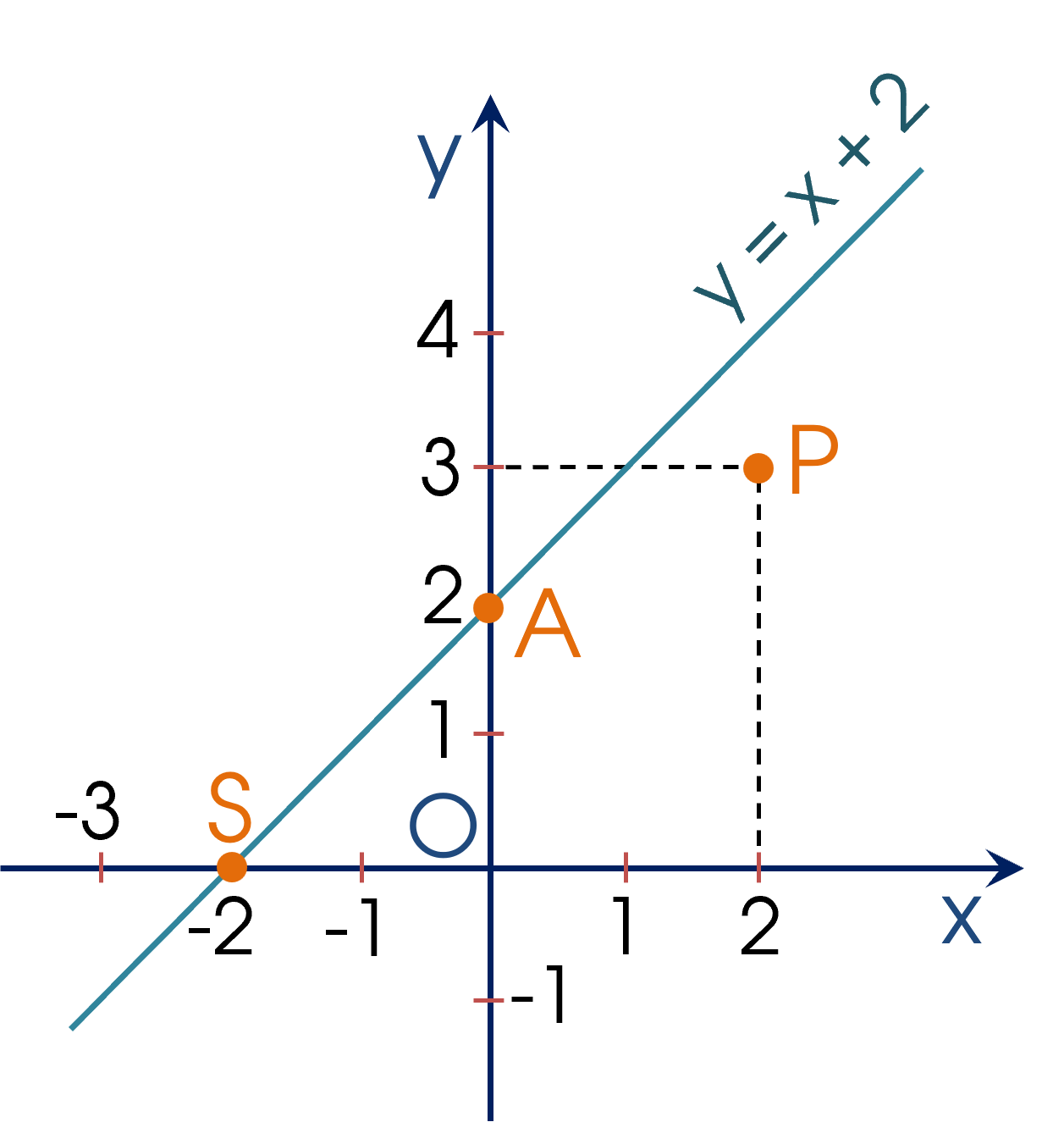
a) Điểm nào sau đây thuộc/ không thuộc đồ thị của hàm số?

     $A(0;2)$; $S(-2;0)$ và $P(2;3)$

b) Điểm $D(2 \, 022 ; 2 \, 023)$ có thuộc đồ thị của hàm số hay không?

Lời giải

a) Quan sát đồ thị của hàm số $y = x + 2$, ta thấy:

+ $A(0 ; 2)$, $S(-2 ; 0)$ thuộc đồ thị của hàm số;

+ $P(2 ; 3)$ không thuộc đồ thị của hàm số.

b) Đối với hàm số $y = x + 2$, giá trị của $y$ tương ứng với giá trị $x = 2\,022$ là:

     $y = 2\,022 + 2 = 2\,024 \ne 2\,023$

Vì vậy, điểm $D(2\,022 ; 2\,023)$ không thuộc đồ thị của hàm số.