Bài học cùng chủ đề
Hàm số $y=ax^2 (a \ne 0)$ SVIP
1. Hàm số $y=ax^2 (a \ne 0)$
Nhận biết hàm số $y=ax^2 (a \ne 0)$
Ví dụ 1. Khi thả một vật rơi tự do và bỏ qua sức cản của không khí, quãng đường của chuyển động $s$ (mét) của vật được cho bằng công thức $s=4,9t^2$, trong đó $t$ là thời gian chuyển động của vật (giây).
Ví dụ 2. Công thức tính diện tích $S$ của hình tròn bán kính $r$ là $S= \pi r^2$. Những công thức tính $s$ theo $t$ (trong ví dụ 1), tính $S$ theo $r$ (trong ví dụ 2) biểu thị những hàm số có cùng dạng, gọi là hàm số $y=ax^2 (a \ne 0)$.
Nhận xét.
Hàm số $y=ax^2 (a \ne 0)$ xác định với mọi giá trị $x$ thuộc $\mathbb{R}$.
Ví dụ 3. Cho hàm số $y=\dfrac{3}{2}x^2$. Hoàn thành bảng giá trị sau:
| $x$ | $-3$ | $-2$ | $-1$ | $0$ | $1$ | $2$ | $3$ |
| $y$ | ? | ? | ? | ? | ? | ? | ? |
Lời giải
| $x$ | $-3$ | $-2$ | $-1$ | $0$ | $1$ | $2$ | $3$ |
| $y$ | $\dfrac{27}{2}$ | $6$ | $\dfrac{3}{2}$ | $0$ | $\dfrac{3}{2}$ | $6$ | $\dfrac{27}{2}$ |
2. Đồ thị hàm số $y=ax^2 (a \ne 0)$
Cách vẽ đồ thị hàm số $y=ax^2 (a \ne 0)$
⚡️Bước 1: Lập bảng ghi một số giá trị tương ứng giữa $x$ và $y$.
⚡️Bước 2: Biểu diễn các cặp điểm $(x;y)$ trong bảng giá trị trên trong mặt phẳng $Oxy$ và nối chúng lại để được một đường cong là đồ thị của hàm số $y=ax^2 (a \ne 0)$.
Ví dụ 4. Vẽ đồ thị của hàm số $y=-\dfrac{1}{4}x^2$.
Lời giải
Lập bảng một số giá trị tương ứng giữa $x$ và $y$.
| $x$ | $-4$ | $-2$ | $-1$ | $0$ | $1$ | $2$ | $4$ |
| $y$ | $-4$ | $-1$ |
$-\dfrac{1}{4}$ |
$0$ | $-\dfrac{1}{4}$ | $-1$ | $-4$ |
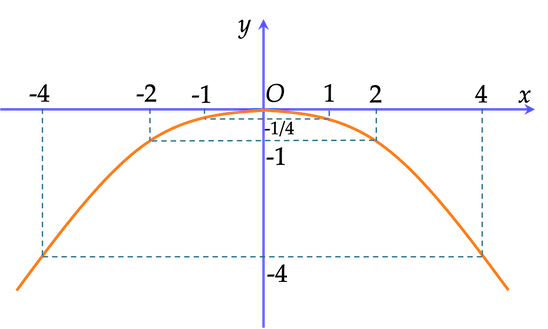
Biểu diễn các điểm $(-4;-4); \, (-2;-1); \, \Big(-1; -\dfrac{1}{4} \Big); \, (0:0); \, (4;-4); \, (2;-1); \, \Big(1; -\dfrac{1}{4} \Big)$ trên mặt phẳng toạ độ $Oxy$ và nối chúng lại ta được đồ thị hàm số $y=-\dfrac{1}{4}x^2$ như hình vẽ.
Nhận biết tính đối xứng của đồ thị hàm số $y=ax^2 (a \ne 0 )$
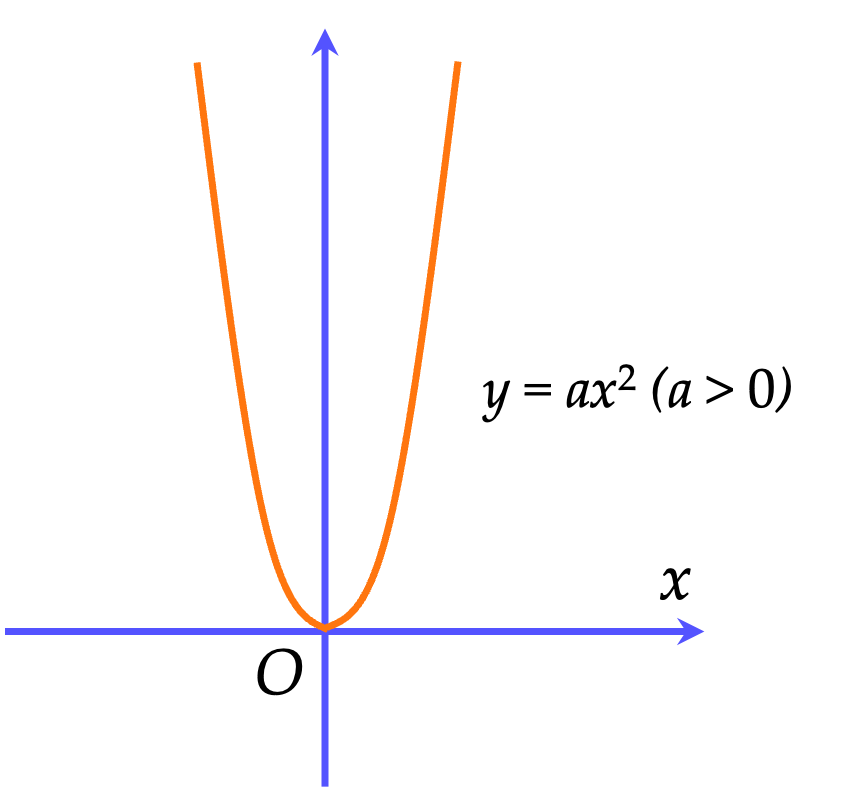
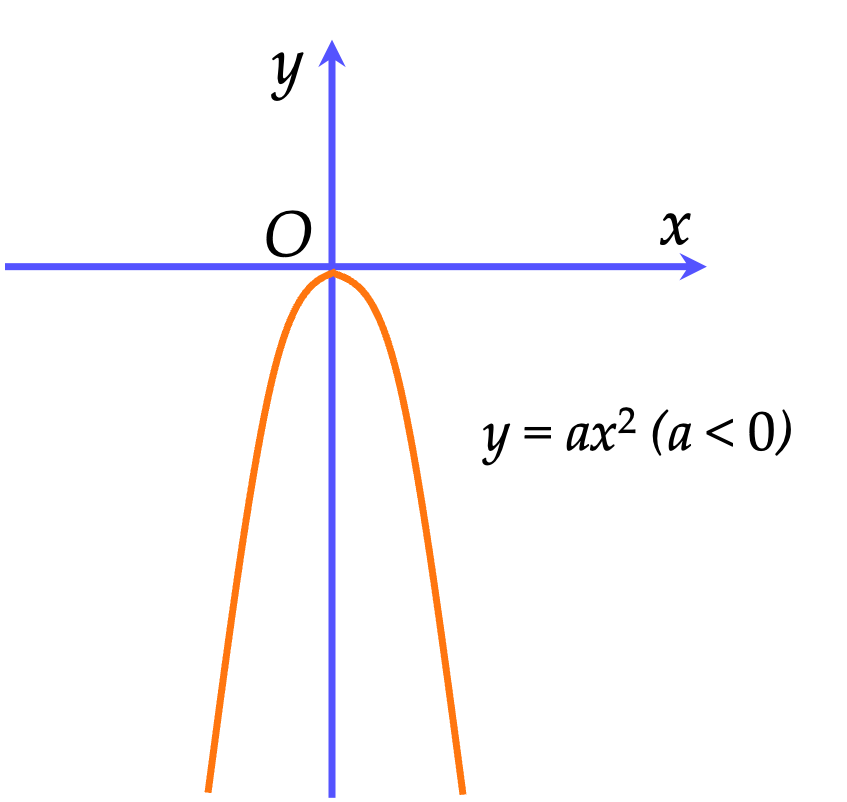
Đồ thị của hàm số $y=ax^2 (a \ne 0)$ là một đường cong, gọi là đường parabol, có các tính chất sau:
⚡️Có đỉnh là gốc toạ độ $O$.
⚡️Có trục đối xứng là $Oy$.
⚡️Nằm phía trên trực hoành nếu $a>0$ và nằm phía dưới trục hoành nếu $a<0$.
Ví dụ 5.
a) Vẽ đồ thị hàm số $y=-2x^2$.
b) Tìm toạ độ các điểm thuộc đồ thị có tung độ bằng $-\dfrac{1}{2}$ và nhận xét về tính đối xứng giữa các điểm đó.
Lời giải
a) Lập bảng một số giá trị tương ứng giữa $x$ và $y$:
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| $y$ | $-8$ | $-2$ | $0$ | $-2$ | $-8$ |
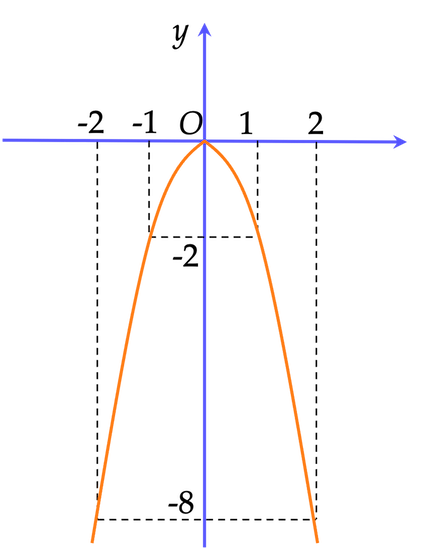
Biểu diễn các điểm $(-2;-8); \, (-1; -2); \, (0:0); \, (2;-8); \, (1; -2)$ trên mặt phẳng toạ độ $Oxy$ và nối chúng lại ta được đồ thị hàm số $y=-2x^2$ như hình vẽ.
b) Ta có: $y=-\dfrac{1}{2}$ nên $-2x^2=-\dfrac{1}{2}$ hay $x^2=\dfrac{1}{4}$.
Suy ra $x=\dfrac{1}{2}$ hoặc $x=-\dfrac{1}{2}$.
Vậy có điểm cần tìm là $\Big( \dfrac{1}{2}; -\dfrac{1}{2} \Big)$ và $\Big( -\dfrac{1}{2}; -\dfrac{1}{2} \Big)$. Hai điểm này đối xứng với nhau qua trục $Oy$.
Chú ý: Hai điểm $(x;y)$ và $(-x;y)$ đối xứng với nhau qua trục tung $Oy$.