Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề số 3 SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Trong hệ trục toạ độ Oxy, elip (E): 16x2+7y2=1 có tiêu cự bằng
Tọa độ các tiêu điểm của hypebol (H):9x2−4y2=1 là
Hùng muốn qua nhà Huy để rủ Huy cùng đến chơi nhà Nam. Từ nhà Hùng đến nhà Huy có 5 con đường đi, từ nhà Huy tới nhà Nam có 8 con đường đi. Hùng có bao nhiêu cách chọn đường đi đến nhà Nam (có đi qua nhà Huy)?
Lớp 10A có 42 học sinh, cần bầu ra một ban cán sự lớp gồm một lớp trưởng, một lớp phó, một thư kí, một sao đỏ và một người không thể giữ hai chức vụ. Có bao nhiêu cách để bầu ra một ban cán sự của lớp 10A?
Số nghiệm của phương trình x2−4=x−2 là
Trong mặt phẳng Oxy, cho hai điểm A(1;1), B(2;3). Một vectơ pháp tuyến của đường trung trực của đoạn thẳng AB là
Trong mặt phẳng tọa độ Oxy, đường thẳng đi qua điểm M(1;−2) và có một vectơ pháp tuyến n=(1;1) có phương trình là
Trong mặt phẳng Oxy, góc giữa hai đường thẳng Δ1:4x+2y−1=0 và Δ2:x+3y−5=0 bằng
Đường tròn tâm I(3;−7), đi qua A(−3;−1) có phương trình là
Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có phương trình x2+(y−3)2=1 và điểm M(1;3) thuộc đường tròn (C). Phương trình tiếp tuyến của đường tròn (C) tại điểm M(1;3) là
Phương trình chính tắc của đường hypebol có tiêu cự bằng 6 và độ dài trục thực A1A2=2a=4 là
Xét phép thử gieo một con xúc xắc cân đối, đồng chất 2 lần liên tiếp. Gọi A là biến cố tổng số chấm xuất hiện 2 lần gieo nhỏ hơn 5. Xác suất của biến cố A là
Cho Δ1:{x=3−ty=2−t; Δ2:{x=1+2ty=1−3t. Khi đó:
(Nhấp vào dòng để chọn đúng / sai)| Δ1 có vectơ chỉ phương u1=(−1;−1) |
|
| Δ2 có vectơ chỉ phương u2=(2;−3) |
|
| Δ1, Δ2 cắt nhau tại điểm có tọa độ (37;32). |
|
| Hai đường thẳng Δ1, Δ2 song song. |
|
Trong mặt phẳng với hệ trục tọa độ Oxy, cho các điểm M(1;−2), N(−3;2) và P(5;0).
(Nhấp vào dòng để chọn đúng / sai)| Nếu đường tròn có tâm là điểm M và có đường kính bằng 2 thì đường tròn có phương trình là (x−1)2+(y+2)2=4. |
|
| Nếu đường tròn có tâm là điểm N và có đường kính bằng 6 thì đường tròn có phương trình là (x+3)2+(y−2)2=9. |
|
| Nếu đường tròn có tâm là điểm P và có đường kính bằng độ dài đoạn MN thì đường tròn có phương trình là (x−5)2+y2=8. |
|
| Nếu đường tròn có đường kính là đoạn NP thì đường tròn có phương trình là (x−1)2+(y−1)2=17. |
|
Một vật chuyển động tròn đều chịu tác động của lực hướng tâm, quỹ đạo chuyển động của vật trong mặt phẳng toạ độ Oxy là đường tròn có phương trình x2+y2=100. Vật chuyển động đến điểm M(8;6) thì bị bay ra ngoài. Trong những giây đầu tiên sau khi vật bay ra ngoài, vật chuyển động trên đường thẳng ax+by+c=0 (với a, b là các số tự nhiên khác 0; a và b nguyên tố cùng nhau) là tiếp tuyến của đường tròn. Tính c.
Trả lời:
Một elip với bán trục lớn a và bán tiêu cự c tỉ số e=ac được gọi là tâm sai của elip. Quỹ đạo của trái đất quanh mặt trời là một elip (E) trong đó mặt trời là một trong các tiêu điểm.
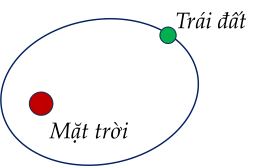
Biết khoảng cách nhỏ nhất và lớn nhất giữa mặt trời và trái đất lần lượt là 147 triệu km, 152 triệu km. Tính tâm sai của elip (E). (Làm tròn kết quả tới chữ số thập phân thứ ba)
Trả lời:
Một lô hàng có 14 sản phẩm, trong đó có đúng 2 phế phẩm. Chọn ngẫu nhiên 8 sản phẩm trong lô hàng đó. Tính xác suất của biến cố "Trong 8 sản phẩm được chọn có không quá 1 phế phẩm". (Làm tròn kết quả đến chữ số thập phân thứ hai)
Trả lời:
Để chụp toàn cảnh, ta có thể sử dụng một gương hypebol. Máy ảnh được hướng về phía đỉnh của gương và tâm quang học của máy ảnh được đặt tại một tiêu điểm của gương (xem hình).
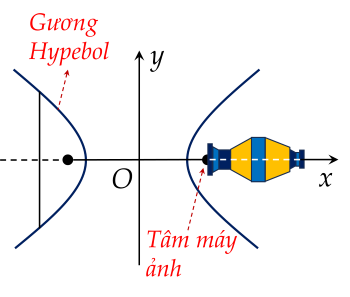
Tìm khoảng cách từ quang tâm của máy ảnh đến đỉnh của gương, biết rằng phương trình cho mặt cắt của gương là 25x2−16y2=1. (Làm tròn đến chữ số thập phân thứ hai)
Trả lời:
Một hộp có 15 quả cầu trắng, 5 quả cầu đen. Xét phép thử chọn ngẫu nhiên 3 quả cầu.
(Nhấp vào dòng để chọn đúng / sai)| Không gian mẫu của phép thử là 1140. |
|
| Xác suất để chọn được 2 quả cầu trắng là 767. |
|
| Xác suất để chọn được ít nhất một quả cầu đen là 228137. |
|
| Xác suất để chọn được 3 quả cầu thuộc hai loại khác nhau là 7635. |
|
Lớp 11A có 7 học sinh nữ và 13 học sinh nam. Cô chủ nhiệm chọn ra 5 bạn để tham gia văn nghệ.
(Nhấp vào dòng để chọn đúng / sai)| Xác suất để cô chủ nhiệm chọn được 5 học sinh nữ là 1550421. |
|
| Xác suất để cô chủ nhiệm chọn được đúng 3 học sinh nam là C205C133.C72. |
|
| Xác suất để cô chủ nhiệm chọn được ít nhất 1 học sinh nữ là 5168429. |
|
| Xác suất để cô chủ nhiệm số học sinh nữ nhiều hơn số học sinh nam là 77521603. |
|
Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua vào một chiếc là 27 triệu đồng và bán ra với giá là 31 triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm 1 triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ tăng thêm 200 chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu để sau khi đã thực hiện giảm giá, lợi nhuận thu được sẽ là cao nhất?
Trả lời: triệu đồng
Một người có 500 triệu đồng gửi tiết kiệm ngân hàng với lãi suất 7,2%/năm. Với giả thiết sau mỗi tháng người đó không rút tiền thì số tiền lãi được nhập vào số tiền ban đầu. Đây được gọi là hình thức lãi kép. Biết số tiền cả vốn lẫn lãi T sau n tháng được tính bởi công thức T=T0(1+r)n, trong đó T0 là số tiền gửi lúc đầu và r là lãi suất của một tháng. Dùng tổng hai số hạng đầu tiên trong khai triển của nhị thức Newton, tính gần đúng số tiền người đó nhận được (cả gốc lẫn lãi) sau 6 tháng.
Trả lời: triệu đồng.
