Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề số 1 (cấu trúc mới 2025) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Trong mặt phẳng Oxy, cho elip (E) có một tiêu điểm là F1(−3;0) và đi qua điểm M(−3;21). Phương trình chính tắc của elip (E) là
Xét phép thử bốc 2 thẻ từ một hộp đựng 9 thẻ đánh số từ 1 đến 9 và A là biến cố xuất bốc được ít nhất 1 thẻ chẵn. Xác suất của biến cố A là
Một hộp chứa 9 viên bi được đánh số từ 1 đến 9. Bạn Đô bốc ngẫu nhiên hai viên bi từ trong hộp. Xác suất để bạn Đô bốc được hai viên bi đều đánh số lẻ bằng
Trong mặt phẳng Oxy, gọi (H) là hypebol có một tiêu điểm là F1(−10;0) và đi qua điểm A(4;−2).
(Nhấp vào dòng để chọn đúng / sai)| Tiêu điểm còn lại của hypebol (H) là F2(10;0). |
|
| Hypebol (H) có tiêu cự bằng 10. |
|
| Giá trị tuyệt đối của hiệu các khoảng cách từ mỗi điểm thuộc hypebol (H)đến hai tiêu điểm bằng 42. |
|
| Phương trình chính tắc của hypebol (H) là 8x2−2y2=1. |
|
Mẫu số liệu sau cho biết sĩ số của 5 lớp khối 10 tại một trường Trung học là
40; 45; 46; 41; 43.
(Nhấp vào dòng để chọn đúng / sai)| Khoảng biến thiên của mẫu số liệu là R=3. |
|
| Phương sai của mẫu số liệu là s2=5,2. |
|
| Trung vị của mẫu số liệu là Q2=46. |
|
| Số trung bình của mẫu số liệu là x=43. |
|
Parabol (P):y2=8x có tiêu điểm
Hùng muốn qua nhà Huy để rủ Huy cùng đến chơi nhà Nam. Từ nhà Hùng đến nhà Huy có 5 con đường đi, từ nhà Huy tới nhà Nam có 8 con đường đi. Hùng có bao nhiêu cách chọn đường đi đến nhà Nam (có đi qua nhà Huy)?
Một thùng giấy trong đó có 7 hộp đựng bút màu khác nhau. Số cách chọn hai hộp từ 7 hộp đựng bút trên là
Hệ số của x3 trong khai triển Newton biểu thức (2x+1)5 bằng
Trong mặt phẳng Oxy, côsin góc giữa hai đường thẳng d:5x+y−3=0 và d′:−1x+5y=1 bằng
Phương trình nào sau đây không phải là phương trình đường tròn?
Cho số gần đúng a=1000 với sai số tuyệt đối Δa=20. Sai số tương đối của a xấp xỉ
Tứ phân vị thứ ba của mẫu số liệu 5;13;5;7;10;2;3 là
Trong trận đá bóng giữa đội tuyển VIỆT NAM và THÁI LAN, hành động nào sau đây là phép thử ngẫu nhiên?
Trong mặt phẳng với hệ trục tọa độ Oxy, cho các điểm M(1;−2), N(−3;2) và P(5;0).
(Nhấp vào dòng để chọn đúng / sai)| Nếu đường tròn có tâm là điểm M và có đường kính bằng 2 thì đường tròn có phương trình là (x−1)2+(y+2)2=4. |
|
| Nếu đường tròn có tâm là điểm N và có đường kính bằng 6 thì đường tròn có phương trình là (x+3)2+(y−2)2=9. |
|
| Nếu đường tròn có tâm là điểm P và có đường kính bằng độ dài đoạn MN thì đường tròn có phương trình là (x−5)2+y2=8. |
|
| Nếu đường tròn có đường kính là đoạn NP thì đường tròn có phương trình là (x−1)2+(y−1)2=17. |
|
Từ các số {0;1;2;3;4;5;6;7;8} có thể lập được bao nhiêu số tự nhiên có 5 chữ số khác nhau sao cho luôn có mặt 3 chữ số 0; 1; 2 và ba số này đứng cạnh nhau?
Trả lời:
Cho đường tròn (C):(x−2)2+y2=54 và các đường thẳng d1:x−y=0, d2:x−7y=0. Đường tròn (C′) có tâm I nằm trên đường tròn (C) và tiếp xúc với d1,d2 có bán kính bằng bao nhiêu? (Làm tròn kết quả đến chữ số hàng phần trăm)
Trả lời:
Phương trình chính tắc của elip đi qua điểm M(23;2) và M nhìn hai tiêu điểm của elip dưới một góc vuông có dạng (E):mx2+ny2=1. Tính m−n.
Trả lời:
Thùng I chứa các quả bóng được đánh số 1;2;3;4. Thùng II chứa các quả bóng được đánh số 1;2;3;4. Lấy ra ngẫu nhiên một quả bóng ở mỗi thùng. Tính xác suất để quả bóng lấy ra ở thùng I được đánh số lớn hơn quả bóng lấy ra ở thùng II. (Làm tròn kết quả đến chữ số hàng phần nghìn)
Trả lời:
Trong tủ giày có 4 đôi giày khác loại. Bạn Đô lấy ra ngẫu nhiên 2 chiếc. Biết xác suất để lấy ra được một đôi giày hoàn chỉnh là x1. Tìm x.
Trả lời:
Để chụp toàn cảnh, ta có thể sử dụng một gương hypebol. Máy ảnh được hướng về phía đỉnh của gương và tâm quang học của máy ảnh được đặt tại một tiêu điểm của gương (xem hình).
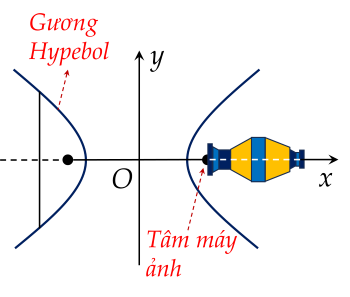
Tìm khoảng cách từ quang tâm của máy ảnh đến đỉnh của gương, biết rằng phương trình cho mặt cắt của gương là 25x2−16y2=1. (Làm tròn đến chữ số thập phân thứ hai)
Trả lời:
Bộ bài tú lơ khơ có 52 quân bài, trong đó gồm 13 tứ quý là A; 2; 3; ...; 10; J; Q và K. Rút ngẫu nhiên ra 4 quân bài.
(Nhấp vào dòng để chọn đúng / sai)| Xác suất của biến cố A: "Rút ra được tứ quý Át" là 521. |
|
| Xác suất của biến cố B: "Rút ra được hai quân Át, hai quân K" là 27072536. |
|
| Xác suất của biến cố C: "Rút ra được ít nhất một quân Át" là 5414538916. |
|
| Xác suất của biến cố D: "Rút ra được 4 quân trong đó có đúng 2 quân ở cùng một tứ quý và hai quân còn lại ở hai tứ quý khác nhau" là 27072582368. |
|
