Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

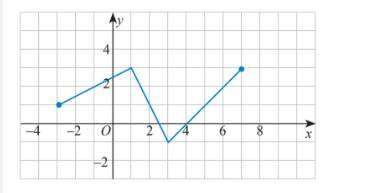
a) Từ đồ thị ta thấy hàm số xác định trên [-3;7]
+) Trên khoảng (-3; 1): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (-3; 1).
+) Trên khoảng (1; 3): đồ thị có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (1; 3).
+) Trên khoảng (3; 7): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (3; 7).
b) Xét hàm số \(y = 5{x^2}\) trên khoảng (2; 5).
Lấy \({x_1},{x_2} \in (2;5)\) là hai số tùy ý sao cho \({x_1} < {x_2}\).
Do \({x_1},{x_2} \in (2;5)\) và \({x_1} < {x_2}\) nên \(0 < {x_1} < {x_2}\), suy ra \({x_1}^2 < {x_2}^2\) hay \(5{x_1}^2 < 5{x_2}^2\)
Từ đây suy ra \(f({x_1}) < f({x_2})\)
Vậy hàm số đồng biến (tăng) trên khoảng (2; 5).

Trục đối xứng của hàm số là: \(x = \frac{5}{2}.\)
Vì \(a = 1 > 0\) nên hàm số đồng biến trên khoảng \(\left( {\frac{5}{2}; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ;\frac{5}{2}} \right).\)
Chọn C.

Với x 1 ≠ x 2 ta có:
f x 2 - f x 1 x 2 - x 1 = - x 2 2 + 4 x 2 - 2 - - x 1 2 + 4 x 1 - 2 x 2 - x 1 = - x 2 2 - x 1 2 + 4 ( x 2 - x 1 ) x 2 - x 1 = - x 2 + x 1 + 4 .
· Với x 1 , x 2 ∈ - ∞ ; 2 thì x1 < 2; x2 <2 nên x 1 + x 2 < 4 ⇒ - x 1 + x 2 + 4 > 0 nên f(x) đồng biến trên khoảng - ∞ ; 2 .
· · Với x 1 , x 2 ∈ 2 ; + ∞ thì x1>2; x2 >2 nên x 1 + x 2 > 4 ⇒ - x 1 + x 2 + 4 < 0 nên f(x) nghịch biến trên khoảng 2 ; + ∞ .
Vậy đáp án là A.
Nhận xét: Với 4 phương án trả lời cho ta biết f(x) đồng biến hoặc nghịch biến trên mỗi khoảng - ∞ ; 2 và 2 ; + ∞ .
Vì vậy, ta lấy hai giá trị bất kì x 1 < x 2 thuộc mỗi khoảng rồi so sánh f x 1 và f x 2 . Chẳng hạn x 1 = 0 ; x 2 = 1 có f 0 = - 2 ; f 1 = 1 nên f 0 < f 1 , suy ra f(x) đồng biến trên khoảng - ∞ ; 2 .

Vẽ đồ thị \(y = 3x + 1;y = - 2{x^2}\)

a) Trên \(\mathbb{R}\), đồ thị \(y = 3x + 1\) đi lên từ trái sang phải, như vậy hàm số \(y = 3x + 1\) đồng biến trên \(\mathbb{R}\)
b) Trên khoảng \(\left( { - \infty ;0} \right)\), đồ thị \(y = - 2{x^2}\)đi lên từ trái sang phải với mọi \(x \in \left( { - \infty ;0} \right)\) , như vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\)
Trên khoảng \(\left( {0; + \infty } \right)\), đồ thị \(y = - 2{x^2}\)đi xuống từ trái sang phải với mọi \(x \in \left( {0; + \infty } \right)\) , như vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\)
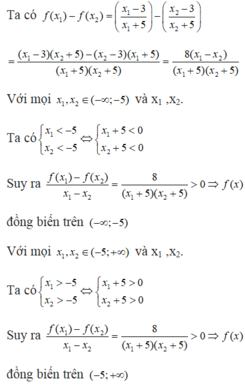

Đáp án A