Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi H là trung điểm của AB. Do ∆ S A B đều nên S H ⊥ A B và S H = A B 3 2 = 2 3 .
Mà S A B ⊥ ( A B C D ) nên S H ⊥ ( A B C D ) .

Từ d S , A B C D d M , A B C D = S D M D = 2 ⇒ d M ; ( A B C D ) = d S ; A B C D 2 = S H 2 = 3 .
Ta có S ∆ P C N = 1 2 P C . P N = 1 2 . B C 2 . C D 2 = 1 2 . 4 2 . 4 2 = 2 (đvdt).
→ V M . P C N = 1 3 . d M ; ( A B C D ) . S ∆ P C N = 1 3 . 3 . 2 = 2 3 3 (đvdt) .
→ y = 2 3 3
Lại có S A B P N = S A B C D - S ∆ P C N = 4 2 - 1 2 . 2 . 2 - 1 2 . 4 . 2 = 10 (đvdt)
V S . A B P N = 1 3 . S H . S A B P N = 1 3 . 2 3 . 10 = 20 3 3 (đvdt) .
* Phương án A:
x 2 + 2 x y - y 2 = 20 3 3 2 + 2 . 20 3 3 . 20 3 3 - 2 3 3 2 = 476 3 < 160
* Phương án B:
x 2 - 2 x y + 2 y 2 = 20 3 3 2 - 2 . 20 3 3 . 20 3 3 + 2 2 3 3 2 = 328 3 > 109
* Phương án C:
x 2 + x y - y 4 = 20 3 3 2 + 20 3 3 . 20 3 3 - 2 3 3 4 = 1304 9 < 145
* Phương án D:
x 2 - x y + y 4 = 20 3 3 2 - 20 3 3 . 20 3 3 + 2 3 3 4 = 1096 9 < 125

Đáp án B
Đặt a=2. Gọi H là trung điểm của BC khi đó A H ⊥ B C D H ⊥ B C
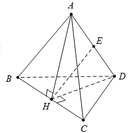
Suy ra B C ⊥ A H D và ta có A H = D H = a 3 2
Gọi E là trung điểm của AD do tam giác AHD cân nên
H E ⊥ A D ⇒ H E = A H 2 − A E 2 = 3 a 2 4 − x 2 4
Ta có V A B C D = V B . A H D + V C . A H D
= 1 3 B C . S A H D = 1 3 a . 1 2 H E . A D
Lại có:
3 a 2 4 − x 2 4 . x = 2 3 a 2 4 − x 2 4 . x 2 ≤ 3 a 2 4 − x 2 4 + x 2 4
= 3 a 2 4 ⇒ V A B C D ≤ a 3 8 ⇒ V max = a 3 8 .
Dấu bằng xảy ra 3 a 2 = 2 x 2 ⇔ x = a 6 2 = 6
Cách 2: Nhận xét V max ⇔ S A H D lớn nhất 1 2 A H . D H sin A H D ⏜ = 3 a 2 8 . sin A H D ⏜ ≤ 3 a 2 8

Đáp án C
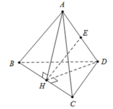
Gọi H là trung điểm BC khi đó A H ⊥ B C D H ⊥ B C
SUY RA B C ⊥ A H D và ta có A H = D H = a 3 2
Gọi E là trung điểm của AD do tam giác AHD cân nên
H E ⊥ A D ⇒ H E = A H 2 − A E 2 = 3 a 2 4 − x 2 4
Ta có V A B C D = V B A H D + V C A H D = 1 3 B C . S A H D = 1 3 a 1 2 H E . A D
Lại có
3 a 2 4 − x 2 4 . x = 2. 3 a 2 4 − x 2 4 . x 2 ≤ 3 a 2 4 − x 2 4 + x 2 4 = 3 a 2 4 ⇒ V A B C D ≤ a 3 8 ⇒ V m a x = a 3 8
Dấu bằng xảy ra khi và chỉ khi 3 a 2 = 2 x 2 ⇔ x = a 6 2 = 3 2

Đáp án C
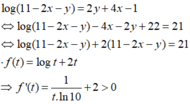
Suy ra f(t) đồng biến trên TXĐ và pt f(t) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 − 2 x − y = 10 ⇒ y = 1 − 2 x ⇒ P = 16 x 2 ( 1 − 2 x ) − 2 x ( 3 − 6 x + 2 ) − 1 + 2 x + 5 = − 32 x 3 + 28 x 2 − 8 x + 4 P ' = − 96 x 2 + 56 x − 8 P ' = 0 ⇔ x = 1 4 x = 1 3 P ( 0 ) = 4 , P ( 1 3 ) = 88 27 , P ( 1 4 ) = 13 4 , P ( 1 2 ) = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17

Đáp án C
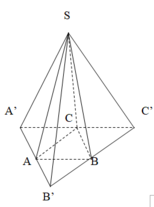
Dựng hình chóp SA’B’C’ sao cho A là trung điểm A’B’, B là trung điểm B’C’, C là trung điểm A’C’.
⇒ S A = 1 2 A ' B ' , S B = 1 2 B ' C ' , S C = 1 2 A ' C '
Suy ra SA’,SB’,SC’ đôi một vuông góc với nhau
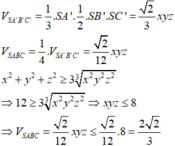

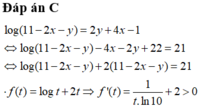
Suy ra f(t) đồng biến trên TXĐ và pt f ( t ) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 - 2 x - y = 10 ⇒ y = 1 - 2 x ⇒ P = 16 x 2 1 - 2 x - 2 x 3 - 6 x + 2 - 1 + 2 x + 5 = - 32 x 3 + 28 x 2 - 8 x + 4 P ' = - 96 x 2 + 56 x - 8 P ' = 0 ⇔ [ x = 1 4 x = 1 3 P 0 = 4 , P 1 3 = 88 27 , P 1 4 = 13 4 , P 1 2 = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17




Đáp án là A