Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

O C A B N M K M'
a.Gọi M' là giao điểm của CM với đường tròn. Do C thuộc AO nên ta thấy ngay cung MB \(\ge\) cung AM'.
Lại có \(\widehat{CMB}=\frac{sđ\left(BM'\right)}{2}=\frac{180^o-sđ\left(AM'\right)}{2}\); \(\widehat{MBC}=\frac{sđ\left(AM\right)}{2}=\frac{180^o-sđ\left(BM\right)}{2}\)
Vậy nê \(\widehat{CMB}\ge\widehat{MBC}\Rightarrow BC\ge CM.\)
b. Ta thấy tam giác CMN vuông tại C, K là trung điểm MN nên theo định lý về đường trung tuyến ứng với cạnh huyền trong tam giác vuông, ta có: CK = NK = KM.
Lại có do K là trung điểm MN nên \(OK\perp MN.\)
Vậy thì \(CK^2+OK^2=NK^2+OK^2=ON^2=\left(\frac{AB}{2}\right)^2=\frac{AB^2}{4}\) không đổi (đpcm).
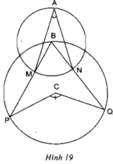


Đường tròn tâm B có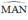 là góc nội tiếp chắn cung
là góc nội tiếp chắn cung 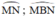 là góc ở tâm chắn cung
là góc ở tâm chắn cung 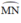
Đường tròn tâm C có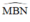 là góc nội tiếp chắn cung
là góc nội tiếp chắn cung 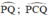 là góc ở tâm chắn cung
là góc ở tâm chắn cung