A....">

📢 OLM ra mắt OLM EduHub - Dịch vụ giáo dục theo yêu cầu! Xem chi tiết tại đây 🚀

🎯Bài kiểm tra ĐGNL đầu hè miễn phí cho học sinh

Hướng dẫn xuất báo cáo, thống kê dành cho nhà trường. Xem ngay!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
T
Tdq_S.Coups
31 tháng 8 2019
C/Minh đẳng thức: a) \(\left(\frac{\sqrt{a}+2}{a+2\sqrt{a}+1}-\frac{\sqrt{a}-2}{a-1}\right).\frac{\sqrt{a}+1}{\sqrt{a}}=\frac{2}{a-1}\) (với a>0, b>0, a≠b) b)\(\frac{2}{\sqrt{ab}}:\left(\frac{1}{\sqrt{a}}-\frac{1}{\sqrt{b}}\right)^2-\frac{a+b}{\left(\sqrt{a}-\sqrt{b}\right)^2}=-1\) (với a>0, b>0,a≠b) c) \(\frac{2\sqrt{a}+3\sqrt{b}}{\sqrt{ab}+2\sqrt{a}-3\sqrt{b}-6}-\frac{6-\sqrt{ab}}{\sqrt{ab}+2\sqrt{a}+3\sqrt{b}+6}=\frac{a+9}{a-9}\) (với a≥0,...
Đọc tiếp

C/Minh đẳng thức:

a) \(\left(\frac{\sqrt{a}+2}{a+2\sqrt{a}+1}-\frac{\sqrt{a}-2}{a-1}\right).\frac{\sqrt{a}+1}{\sqrt{a}}=\frac{2}{a-1}\) (với a>0, b>0, a≠b)

b)\(\frac{2}{\sqrt{ab}}:\left(\frac{1}{\sqrt{a}}-\frac{1}{\sqrt{b}}\right)^2-\frac{a+b}{\left(\sqrt{a}-\sqrt{b}\right)^2}=-1\) (với a>0, b>0,a≠b)

c) \(\frac{2\sqrt{a}+3\sqrt{b}}{\sqrt{ab}+2\sqrt{a}-3\sqrt{b}-6}-\frac{6-\sqrt{ab}}{\sqrt{ab}+2\sqrt{a}+3\sqrt{b}+6}=\frac{a+9}{a-9}\) (với a≥0, b≥0,a≠9)
#Hỏi cộng đồng OLM #Toán lớp 9
0
HQ
Hồ Quang Phước
25 tháng 7 2018
rút gọn biểu thức A=\(\dfrac{\sqrt{a}-1}{a\sqrt{a}-a+\sqrt{a}}:\dfrac{1}{a^2+\sqrt{a}}\) với a >0 B=\(\dfrac{\sqrt{a}+\sqrt{b}-1}{a+\sqrt{ab}}+\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\left(\dfrac{\sqrt{b}}{a-\sqrt{ab}}+\dfrac{\sqrt{b}}{a+\sqrt{ab}}\right)\) với a>0 b>0 và a khác b C=\(\dfrac{a\sqrt{b}+b}{a-b}.\sqrt{\dfrac{ab+b^2-2\sqrt{ab^3}}{a\left(a+2\sqrt{b}\right)+b}}:\dfrac{1}{\sqrt{a}+\sqrt{b}}\) với...
Đọc tiếp

rút gọn biểu thức

A=\(\dfrac{\sqrt{a}-1}{a\sqrt{a}-a+\sqrt{a}}:\dfrac{1}{a^2+\sqrt{a}}\) với a >0

B=\(\dfrac{\sqrt{a}+\sqrt{b}-1}{a+\sqrt{ab}}+\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\left(\dfrac{\sqrt{b}}{a-\sqrt{ab}}+\dfrac{\sqrt{b}}{a+\sqrt{ab}}\right)\) với a>0 b>0 và a khác b

C=\(\dfrac{a\sqrt{b}+b}{a-b}.\sqrt{\dfrac{ab+b^2-2\sqrt{ab^3}}{a\left(a+2\sqrt{b}\right)+b}}:\dfrac{1}{\sqrt{a}+\sqrt{b}}\) với a>b>0
#Hỏi cộng đồng OLM #Toán lớp 9
1
NL
Nguyễn Lê Phước Thịnh
30 tháng 8 2022

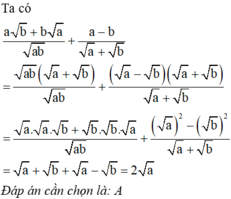
a: \(=\dfrac{\sqrt{a}-1}{\sqrt{a}\left(a-\sqrt{a}+1\right)}\cdot\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{1}\)

\(=a-1\)

b: \(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\cdot\left(\dfrac{\sqrt{b}}{\sqrt{a}\left(\sqrt{a}-\sqrt{b}\right)}+\dfrac{\sqrt{b}}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}\right)\)

\(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\cdot\dfrac{\sqrt{ab}+b+\sqrt{ab}-b}{\sqrt{a}\left(a-b\right)}\)

\(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}=\dfrac{1}{\sqrt{a}}\)

c: \(=\dfrac{a\sqrt{b}+b}{a-b}\cdot\sqrt{\dfrac{ab+b^2-2b\sqrt{ab}}{a^2+2a\sqrt{b}+b}}\cdot\left(\sqrt{a}+\sqrt{b}\right)\)

\(=\dfrac{\sqrt{b}\left(a+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\cdot\sqrt{\dfrac{b\left(\sqrt{a}-\sqrt{b}\right)^2}{\left(a+\sqrt{b}\right)^2}}\)

\(=\dfrac{\sqrt{b}\left(a+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\cdot\dfrac{\sqrt{b}\left(\sqrt{a}-\sqrt{b}\right)}{a+\sqrt{b}}=b\)

Đúng(0)
NH
nguyen hieu
4 tháng 7 2018 - olm

c​hứng minh bất đẳng thức \(\frac{1}{\sqrt{AB}}>\frac{2}{A+B}với\) A,B>0 A khác B
#Hỏi cộng đồng OLM #Toán lớp 9
1
KT
Không Tên
4 tháng 7 2018

Áp dụng BĐT AM-GM ta có:

\(\frac{1}{\sqrt{AB}}=\frac{2}{2\sqrt{AB}}\ge\frac{2}{A+B}\)(đpcm)

p/s: tham khảo

       chúc bn hk tốt

Đúng(0)
CD
Cỏ dại
22 tháng 6 2019 - olm

C/minh  bất đẳng thức sau:

\(a+b>4\) với \(a,b>0\) và \(a+b< ab\)
#Hỏi cộng đồng OLM #Toán lớp 9
0
HA
%Hz@
24 tháng 12 2019 - olm

câu 1

a) Cho a ≥ 0, b ≥ 0. Chứng minh bất đẳng thức Cauchy:\(\frac{a+b}{2}\ge\sqrt{ab}\)

b) Cho a, b, c > 0. Chứng minh rằng:\(\frac{bc}{a}+\frac{ca}{b}+\frac{ab}{c}\ge a+b+c\)

c) Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab.
#Hỏi cộng đồng OLM #Toán lớp 9
3
NV
Nguyễn Văn Tuấn Anh
24 tháng 12 2019

a) \(\frac{a+b}{2}\ge\sqrt{ab}\)

\(\Leftrightarrow\frac{a^2+2ab+b^2}{4}-ab\ge0\)

\(\Leftrightarrow a^2-2ab+b^2\ge0\)

\(\Leftrightarrow\left(a-b\right)^2\ge0\) (luôn đúng \(\forall a,b\) )

=>đpcm

Đúng(0)
ZC
zZz Cool Kid_new zZz
25 tháng 12 2019

Cô si

\(\frac{bc}{a}+\frac{ca}{b}\ge2\sqrt{\frac{bc}{a}\cdot\frac{ca}{b}}=2c\)

\(\frac{ca}{b}+\frac{ab}{c}\ge2\sqrt{\frac{ca}{b}\cdot\frac{ab}{c}}=2a\)

\(\frac{ab}{c}+\frac{bc}{a}\ge2\sqrt{\frac{ab}{c}\cdot\frac{bc}{a}}=2b\)

Cộng lại ta có:

\(2\left(\frac{bc}{a}+\frac{ca}{b}+\frac{ab}{c}\right)\ge2\left(a+b+c\right)\Rightarrowđpcm\)

Đúng(0)
ND
Nguyễn Diệu Linh
24 tháng 7 2018

Chứng minh đẳng thức:

\(\dfrac{a\sqrt{b}+b}{a-b}.\sqrt{\dfrac{ab+b^2-2\sqrt{ab^2}}{a\left(a+2\sqrt{b}+b\right)}}\left(\sqrt{a}+\sqrt{b}\right)=b\) (với a > b > 0)
#Hỏi cộng đồng OLM #Toán lớp 9
0
HN
hội những người háu ăn
17 tháng 4 2019 - olm

với a>0 , b> 0 ,  c>0  .CM bất đẳng thức:

\(\frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}\ge a+b+c\)
#Hỏi cộng đồng OLM #Toán lớp 9
2
CT
Cố Tử Thần
17 tháng 4 2019

trả lời

dùng bất đẳng thức cosi cho 2 số ko âm

sử dụng cộng mỗi cặp trên

đc 3 cặp

cộng lại là ra

Đúng(0)
A
Aug.21
17 tháng 4 2019

ta có : \(\frac{ab}{c}+\frac{ca}{b}\ge2a;\frac{bc}{a}+\frac{ca}{b}\ge2c\)

Do đó : \(\frac{ab}{c}+\frac{bc}{a}+\frac{ab}{c}+\frac{ca}{b}+\frac{bc}{a}+\frac{ca}{b}\ge2b+2a+2c\)

\(\Leftrightarrow\frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}\ge a+b+c\)

Đúng(0)
NM
Nguyễn Mai
3 tháng 12 2019 - olm

Chứng minh bất đẳng thức \(\frac{a+b}{a^2+b^2}+\frac{b+c}{b^2+c^2}+\frac{c+a}{c^2+a^2}\le3\)

với a, b,c >0 và a+b+c=ab+bc+ca
#Hỏi cộng đồng OLM #Toán lớp 9
1
T
tth_new
3 tháng 12 2019

Nhìn giả thiết thấy nản quả:(

BĐT \(\Leftrightarrow\Sigma_{cyc}\frac{\left(ab+bc+ca\right)\left(a+b\right)}{a^2+b^2}\le3\left(ab+bc+ca\right)\) (nhân ab +bc +ca vào hai vế)

\(\Leftrightarrow\Sigma_{cyc}\frac{\left(ab+bc+ca\right)\left(a+b\right)}{a^2+b^2}\le3\left(a+b+c\right)\) (chú ý giả thiết ab + bc +ca = a + b +  c)

\(VT=\Sigma_{cyc}\frac{ab\left(a+b\right)}{a^2+b^2}+\Sigma_{cyc}\frac{c\left(a+b\right)^2}{a^2+b^2}\)

\(\le\Sigma_{cyc}\frac{ab\left(a+b\right)}{2ab}+\Sigma_{cyc}\frac{2c\left(a^2+b^2\right)}{a^2+b^2}=3\left(a+b+c\right)\)

Vậy ta có đpcm.Đẳng thức xảy ra khi a = b = c

Đúng(0)
DN
Đặng Nguyễn Khánh Uyên
10 tháng 3 2018

1. Với mọi a, b thuộc R. CMR:

a) \(a^4+b^4\) lớn hơn bằng \(ab^3+a^3b\)

b) \(a^2+b^2+1>_-ab+a+b\)

2. Cho a>0, b>0,c>0 .CMR:

\(ab\left(a+b\right)+bc\left(b+c\right)+ac\left(a+c\right)>_-6abc\)
#Hỏi cộng đồng OLM #Toán lớp 9
2
N
ngonhuminh
10 tháng 3 2018

a^4 +b^4 >= ab^3 +a^3 b (1)
<=> 4a^4 +4b^4 - 4ab(a^2 +b^2) >= 0
<=> [(a^2 +b^2 )^2 - 4ab(a^2 +a^2) +4a^2 b^2 ] +3a^4 +3b^4 -6a^2 b^2 >=0
<=> (a -b )^4 +3(a^4 + b^4 -2a^2 b^2 ) >= 0 (2)
cos (a-b )^4 >= 0
a^4 + b^4 >= 2a^2 b^2 (co si có thể không cần co si cũng được )
=> (2) đúng => (1) đúng => dpcm
b) a^2 +b^2 +1 >= ab +a+b (1)
<=>2a^2 +2b^2 +2 -2ab -2a-2b >=0
<=>[a^2 +b^2 -2ab ] +[a^2 -2a +1] +[b^2 -2b +1 ] >=0
<=>(a -b)^2 +(a-1)^2 + (b-1)^2 >=0 (2)
(2) đúng (1) đúng => dpcm

Đúng(0)
DN
Đặng Nguyễn Khánh Uyên
10 tháng 3 2018

@ngonhuminh

Đúng(0)
PU
Phan Ưng Tố Như
6 tháng 8 2015 - olm

CHỨNG MINH BẤT ĐẲNG THỨC:

a/ \(\sqrt{a-b}>\sqrt{a}-\sqrt{b}\) với a > b >0

b/ \(\sqrt{ab}\ge\sqrt{c\left(a-c\right)}+\sqrt{c\left(b-c\right)}\)với a >c; b >c 
#Hỏi cộng đồng OLM #Toán lớp 9
0
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Yêu cầu VIP