QT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
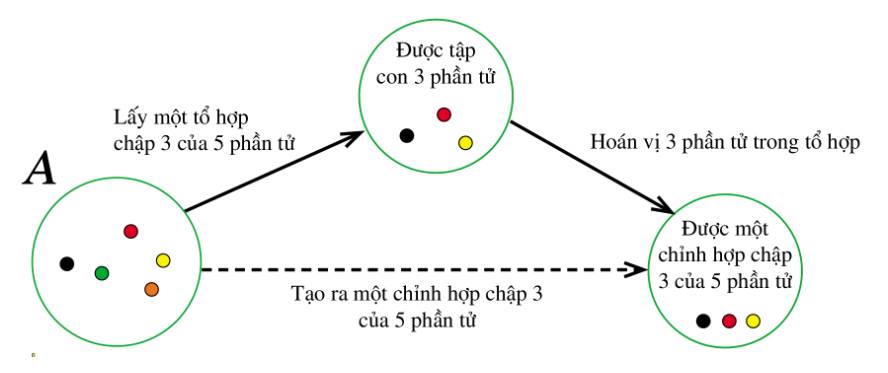
a) Cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A là: Chọn bất kỳ 3 trong 5 phần tử thuộc A ví dụ như \(\left\{ {a;b;c} \right\}\)
b) Cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A là: Chọn bất kỳ 3 trong 5 phần tử thuộc A rồi sắp xếp theo một thứ tự nào ví dụ như ta chọn 3 phần tử a,b,c rồi sắp xếp theo thứ tự ngược của bảng chữ cái \(\left\{ {c;b;a} \right\}\)
c) So sánh: Mỗi tổ hợp chập 3 của 5 phần tử sinh ra 3! chỉnh hợp chập 3 của 5 phần tử vì có 3! hoán vị của 3 phần tử. Vì thế, số chỉnh hợp chập 3 của 5 phần tử nhiều gấp 3! lần số tổ hợp chập 3 của 5 phần tử.
15 tháng 9 2021
Tập hợp C rỗng vì \(x^2+7x+12=0\Leftrightarrow x\in\left\{-3;-4\right\}\notin N\)
\(a,\left\{1;2\right\};\left\{1;3\right\};\left\{2;3\right\}\\ b,\left\{1\right\};\left\{2\right\};\left\{3\right\};\left\{1;2\right\};\left\{1;3\right\};\left\{2;3\right\};\left\{1;2;3\right\}\)
\(X=\left\{1;3\right\}\\ X=\left\{1;2;3\right\}\\ X=\left\{1;3;4\right\}\\ X=\left\{1;3;5\right\}\\ X=\left\{1;2;3;4\right\}\\ X=\left\{1;2;3;5\right\}\\ X=\left\{1;3;4;5\right\}\\ X=\left\{1;2;3;4;5\right\}\)
NM
Nguyễn Minh Châu
VIP
22 tháng 8
Do \(A\) là tập hợp có \(6\) phần tử nên số tập hợp con khác rỗng và khác \(A\) của tập hợp \(A\) là: \(2^{6} - 2 = 62\) (tập hợp con).
Xét tập hợp \(X\) là tập con bất kì trong \(62\) tập hợp con trên và \(T \left(\right. X \left.\right)\) là tổng các phần tử của \(X\).
Tập hợp \(X\) có nhiều nhất \(5\) phần tử thuộc tập hợp \(\left{\right. 0 ; 1 ; 2 ; . . . ; 14 \left.\right}\) nên ta có:
\(0 \leq T \left(\right. X \left.\right) \leq 10 + 11 + 12 + 13 + 14 = 60\).
Như vậy với \(62\) tập hợp con của \(A\) như trên thì tồn tại \(62\) tổng không vượt quá \(60\).
Theo nguyên lí Dirichlet thì tồn tại hai tổng có giá trị bằng nhau. Điều đó chứng tỏ tồn tại hai tập hợp con \(B_{1}\), \(B_{2}\) của tập hợp \(A\) có tổng các phần tử của chúng bằng nhau.
5 tháng 4 2017
1. a) Tập hợp con của A: {a} và \(\varnothing\)
b) Tập hợp con của B: {a}; {b}; {a;b} và \(\varnothing\)
c) Tập hợp con: \(\varnothing\)
2. a) A có 1 phần tử thì A sẽ có: 21=2 (tập hợp con)
b) A có 2 phần tử thì A sẽ có: 22=4 (tập hợp con)
c) A có 3 phần tử thì A sẽ có: 23=8 (tập hợp con)
*Cách tính số tập hợp con: Nếu tập hợp A có n phần tử thì A sẽ có 2n tập hợp con.
15 tháng 9 2023
a: Các tập con là {1}; {2}; {1;2}; \(\varnothing\)
Các tập con có 2 phần tử là {1;2}
b: Các tập con là {1}; {2}; {3}; {1;2}; {2;3}; {1;3}; {1;2;3}; \(\varnothing\)
Các tập con có 2 phần tử là {1;2}; {2;3}; {1;3}
c: Các tập con là {a}; {b}; {c}; {a;b}; {b;c}; {a;c}; {a;b;c}; \(\varnothing\)
Các tập con có 2 phần tử là {a;b}; {b;c}; {a;c}
d: 2x^2-5x+2=0
=>2x^2-4x-x+2=0
=>(x-2)(2x-1)=0
=>x=1/2 hoặc x=2
=>D={1/2;2}
Các tập con là {1/2}; {2}; {1/2;2}; \(\varnothing\)
Các tập con có 2 phần tử là {1/2; 2}
AH
Akai Haruma
Giáo viên
8 tháng 7 2019
Lời giải:
a)
\(\forall x\in\mathbb{Z}\) , để \(\frac{x^2+2}{x}\in\mathbb{Z}|\Leftrightarrow x+\frac{2}{x}\in\mathbb{Z}\Leftrightarrow \frac{2}{x}\in\mathbb{Z}\Leftrightarrow 2\vdots x\)
\(\Rightarrow x\in \left\{\pm 1;\pm 2\right\}\)
Vậy \(A=\left\{-2;-1;1;2\right\}\)
b)
Các tập con của A mà số phần tử nhỏ hơn 3 là:
\(\left\{-2\right\}; \left\{-1\right\};\left\{1\right\};\left\{2\right\}\)
\(\left\{-2;-1\right\}; \left\{-2;1\right\}; \left\{-2;2\right\};\left\{-1;1\right\};\left\{-1;2\right\}; \left\{1;2\right\}\)
AH
Akai Haruma
Giáo viên
18 tháng 6 2019
Lời giải:
a)
\(\forall x\in\mathbb{Z}\) , để \(\frac{x^2+2}{x}\in\mathbb{Z}|\Leftrightarrow x+\frac{2}{x}\in\mathbb{Z}\Leftrightarrow \frac{2}{x}\in\mathbb{Z}\Leftrightarrow 2\vdots x\)
\(\Rightarrow x\in \left\{\pm 1;\pm 2\right\}\)
Vậy \(A=\left\{-2;-1;1;2\right\}\)
b)
Các tập con của A mà số phần tử nhỏ hơn 3 là:
\(\left\{-2\right\}; \left\{-1\right\};\left\{1\right\};\left\{2\right\}\)
\(\left\{-2;-1\right\}; \left\{-2;1\right\}; \left\{-2;2\right\};\left\{-1;1\right\};\left\{-1;2\right\}; \left\{1;2\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 10 2020
a/
\(\Leftrightarrow2m+3\ge m+1\Leftrightarrow m\ge-2\)
b/
Tổng 3 phần tử chẵn \(\Rightarrow\) có các trường hợp:
- Cả 3 phần tử đều chẵn: có đúng 1 tập \(\left\{2;4;6\right\}\)
- 2 phần tử lẻ và 1 phần tử chẵn: chọn 2 phần tử lẻ từ 3 phần tử lẻ có 3 cách, kết hợp với 1 trong 3 phần tử chẵn \(\Rightarrow3.3=9\) tập
Vậy có 10 tập thỏa mãn
Tất cả các tổ hợp chập 2 của 3 phần tử a,b,c là các tập con gồm 2 phần tử được lấy ra từ tập hợp gồm 3 phần từ a,b,c là: \(\left\{ {a;b} \right\},\left\{ {a;c} \right\},\left\{ {b;c} \right\}\)