Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)\(\Delta ABH\) vuông tại H có:
BH2 =AB2 -AH2 =132 -122 =25( ĐL Pytago)
=> BH=5 cm
BC=BH+HC=5+16=21 cm
\(\Delta AHC\) vuông tại H có:
AH2 + HC2 =AC2 ( đl Pytago)
=> AC2 =122 + 162 =20 cm
b) \(\Delta AHB\) vuông tại H có: AB2 = AH2 +BH2 ( ĐL Pytago)
=> BH2 =AB2 - AH2 =132 - 122 =25
=> BH=5 cm
BC= BH+HC=5+16=21 cm
\(\Delta AHC\) vuông tại H có: AC2 = AH2 +HC2 ( đL Pytago)
=> AC2 = 122 + 162 =400
=> AC= 20 cm

câu này mình vừa làm ở bạn Khang Phạm Duy , HÂN nhé
tham khảo .mình giải rất chi tiết

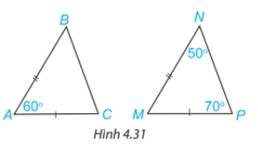
Xét tam giác MNP có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow \widehat M + {50^o} + {70^o} = {180^o}\\ \Rightarrow \widehat M = {60^o}\end{array}\)
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP} (=60^0)\)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

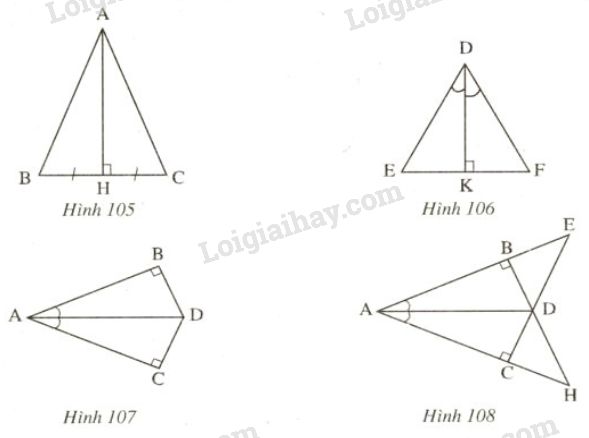
a: Xét ΔBAD và ΔBED có
BA=BE
\(\hat{ABD}=\hat{EBD}\) (BD là phân giác của góc ABE)
BD chung
Do đó: ΔBAD=ΔBED
=>DA=DE
b: ΔBAD=ΔBED
=>\(\hat{BAD}=\hat{BED}\)
=>\(\hat{BED}=90^0\)
=>DE⊥BC
mà AH⊥BC
nên DE//AH
c: Xét ΔMHA và ΔMDK có
MH=MD
\(\hat{MHA}=\hat{MDK}\) (hai góc so le trong, HA//DK)
HA=DK
Do đó: ΔMHA=ΔMDK
=>\(\hat{HMA}=\hat{DMK}\)
mà \(\hat{HMA}+\hat{AMD}=180^0\) (hai góc kề bù)
nên \(\hat{AMD}+\hat{DMK}=180^0\)
=>A,M,K thẳng hàng
Chúng ta sẽ giải từng câu hỏi trong bài toán này.
Câu a) Chứng minh ∆ABD = ∆EBD và AD = ED
- Điều kiện:
- ∆ABC vuông tại A (AB < AC).
- Tia phân giác của góc B cắt AC tại D.
- Trên cạnh BC lấy điểm E sao cho BE = BA.
- Vẽ AH BC tại H.
- Chứng minh:
- Xét các tam giác ∆ABD và ∆EBD:
Vậy, theo Tiêu chuẩn góc-cạnh-góc (Axiom SAS), ta có:
\(\Delta A B D = \Delta E B D\) - Cả hai tam giác ∆ABD và ∆EBD có cạnh chung BD.
- AB = BE (do đề bài cho BE = BA).
- Góc ABD = Góc EBD (vì tia BD là tia phân giác của góc ABC, nên hai góc này bằng nhau).
- Kết luận AD = ED:
- Do ∆ABD = ∆EBD (theo chứng minh trên), nên các cạnh tương ứng của hai tam giác này cũng bằng nhau.
- Vậy, AD = ED.
Câu b) Chứng minh AH // DE
- Xét đoạn AH và DE:
- Từ điều kiện bài toán, chúng ta có điểm H là giao điểm của đường vuông góc AH với cạnh BC, tức là AH ⊥ BC.
- Tia DE được dựng sao cho DE là một đoạn thẳng trong cùng một mặt phẳng với BC, và điểm D là điểm phân giác của góc B.
- Chứng minh AH // DE:
- Vì ∆ABD = ∆EBD (chứng minh ở câu a) nên các góc tương ứng của hai tam giác này cũng bằng nhau. Đặc biệt, ∠BAD = ∠BED.
- Ta có AH ⊥ BC và ∠BAD = ∠BED. Do đó, theo tính chất của góc tạo thành giữa đường vuông góc và đoạn thẳng, ta suy ra rằng AH // DE.
Câu c) Chứng minh A, M, K thẳng hàng
- Định nghĩa các điểm:
- Trên tia DE, lấy điểm K sao cho DK = AH.
- M là trung điểm của DH, tức là:
\(\text{DM} = \text{MH}\)
- Chứng minh A, M, K thẳng hàng:
- Ta đã biết rằng AH // DE, và từ câu b) đã chứng minh rằng AH và DE song song.
- M là trung điểm của DH, tức là DM = MH. Đồng thời, ta có DK = AH (theo giả thiết).
- Vì AH // DE và M là trung điểm của DH, ta có thể sử dụng tính chất của các đường trung tuyến trong tam giác vuông để suy ra rằng các điểm A, M, K nằm trên cùng một đường thẳng.
Kết luận:
- a) ∆ABD = ∆EBD và AD = ED.
- b) AH // DE.
- c) A, M, K thẳng hàng.

a) Có : AB=AC(tg ABC cân tại A)
BD=CE(gt)
=> AB+BD=AC+CE
=> AD=AE
=> Tg ADE cân tại A
\(\Rightarrow\widehat{D}=\widehat{E}=\frac{180^o-\widehat{A}}{2}\)
Lại có : \(\widehat{ABC}=\widehat{ACB}=\frac{180^o-\widehat{A}}{2}\)(tg ABC cân tại A)
\(\Rightarrow\widehat{D}=\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\)
Mà chúng là 2 góc đồng vị
=> BC//DE
b) Có : \(\widehat{CBD}=180^o-\widehat{ABC}\)
\(\widehat{BCE}=180^o-\widehat{ACB}\)
Mà : \(\widehat{ABC}=\widehat{ACB}\)(tg ABC cân tại A)
\(\Rightarrow\widehat{CBD}=\widehat{BCE}\)
- Xét tg BCD và CBE có :
BD=CE(gt)
BC-cạnh chung
\(\widehat{CBD}=\widehat{BCE}\left(cmt\right)\)
=> Tg BCD=CBE(c.g.c)
=> BE=CD(đccm)
c) Có : \(\widehat{KBC}=\widehat{KCB}\)(tg BCD=CBE)
=> Tg KBC cân tại K
- Có : \(\widehat{KDE}=\widehat{ADE}-\widehat{ADC}\)
\(\widehat{KED}=\widehat{AED}-\widehat{AEB}\)
Mà : \(\widehat{AED}=\widehat{ADE}\)(tg ADE cân tại A)
\(\widehat{ADC}=\widehat{AEB}\)(tg BCD=CBE)
\(\Rightarrow\widehat{KED}=\widehat{KDE}\)
=> Tg KDE cân tại K
d) Xét tam giác ABK và ACK có :
AB=AC(tg ABC cân tại A)
AK-cạnh chung
KB=KC(tg KBC cân tại K)
=> Tg ABK=ACK(c.c.c)
=> \(\widehat{BAK}=\widehat{CAK}\)
=> AK là tia pg góc BAC
e) Không thấy rõ đề : DM và EN như thế nào so với BC?

a, theo pytago ta có:
AB2+AC2=BC2 <=> AC=\(\sqrt{10^2-6^2}\)=8 (cm)
so sánh: BAC>ABC>ACB vì BC>AC>AB
b, vì A là trung điểm BD nên CA là trung tuyến của tam giác DBC
mà CA\(\perp\)BD nên CA là đường cao của tam giác DBC
=> CA vừa là trung tuyến vừa là đường cao của tam giác DBC nên DBC cân ở C
Tổng số đo ba góc của tam giác MNP bằng 180o.
=> Tổng ba góc của một tam giác bất kì bằng 180o.