Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình tự vẽ nha AN TRAN DOAN.
Bạn lấy E,F,G,H lần lượt là trung điẻm của AB,BC,CD,DA.
Khi đó, EF, FG, GH, HE có độ dài là \(\sqrt{8}\) (cm)
Vậy chu vi của hình thoi bằng:
\(\sqrt{8}\).4= 8. \(\sqrt{2}\) (cm)
Và: AE= 2(cm)

Xét tam giác ABC có: EB=EA (gt); BF=FC (gt)
⇒⇒EF là đường trung bình của tam giác ABC
⇒⇒EF//AC; EF=1/2AC (1)
Xét tam giác ADC có: AH=HD (gt); CG=DG (gt)
⇒⇒HG là dường trung bình của tam giác ADC
⇒⇒HG//AC; HG=1/2AC (2)
Từ (1) và (2) ⇒⇒EF//HG; EF=HG
⇒⇒EFGH là hình bình hành
Ta có EH là đường trung bình của tam giác ABD
vì AE=EB; AH=HD
⇒⇒EH//BD
mà AC⊥⊥ BD; EH=BD; EF//AC
⇒⇒EF⊥⊥EH hay E=900900
Vậy EFGH là hình chữ nhật.

\(3x^2+7x-20=0\\ < =>3x^2+12x-5x-20=0\\ < =>3x\left(x+4\right)-5\left(x+4\right)=0\\ < =>\left(x+4\right)\left(3x-5\right)=0\\ =>\left\{{}\begin{matrix}x+4=0\\3x-5=0\end{matrix}\right.\\ =>\left\{{}\begin{matrix}x=-4\\x=\dfrac{5}{3}\end{matrix}\right.\)
Vậy: Tập nghiệm của phương trình là \(S=\left\{-4;\dfrac{5}{3}\right\}\)
do câu hỏi của lớp 8 nên mình làm ntn nha:
pt <=> \(3x^2+7x=20\)
<=> \(x^2+\dfrac{7}{3}x=\dfrac{20}{3}\)
<=> \(x^2+2.\dfrac{\dfrac{7}{3}}{2}x+\dfrac{49}{36}-\dfrac{49}{36}=\dfrac{20}{3}\) <=> \(\left(x+\dfrac{7}{6}\right)^2=\dfrac{49}{36}+\dfrac{20}{3}\)
<=> \(\left(x+\dfrac{7}{6}\right)^2=\dfrac{289}{36}\)
<=> x+7/6 = \(\pm\sqrt{\dfrac{289}{36}}\)
<=> \(\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=-4\end{matrix}\right.\)
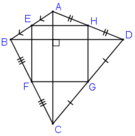
Xét ΔABC có:
E là trung điểm AB (gt)
F là trung điểm AC (gt)
=> EF là đường trung bình ΔABC (ĐN đường TB Δ)
=> EF // AC, EF=\(\dfrac{AC}{2}\) (tính chất đường TB Δ)
Xét ΔADC có:
H là trung điểm AD
G là trung điểm DC
=> HG là đường trung bình ΔADC (ĐN đường TB Δ)
=> HG // AC, HG=\(\dfrac{BC}{2}\) (tính chất đường TB Δ)
Ta có: EF // AC, HG // AC
EF=\(\dfrac{AC}{2}\),HG=\(\dfrac{AC}{2}\)
=> EF // HG, EF = HG
Xét tứ giác EFGH có:
EF // HG
EF = HG
=> EFGH là hình bình hành (dhnb)
ok cảm ơn bn