Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu trong 11 số tự nhiên đó có 1 số chia hết cho 10 thì bài toán đã được chứng minh.
Nếu trong 11 số đã cho, không có số nào chia hết cho 10, ta đặt:
A1= 1
A2= 1+2
A3= 1+2+3
...
A11= 1+2+3+...+10+11
Ta biết rằng, trong 1 phép chia cho 10, ta luôn nhận được 10 số dư từ 0->9
Vì ta có 11 dãy số nên ít nhất có 2 dãy số có cùng số dư trong phép chia cho 10.
Giả sử, dãy Bm và Bn có cùng số dư trong phép chia cho 10 thì ( Bm - Bn ) chia hết cho 10. => đpcm.

a) Gọi các số hạng của dãy trên lần lượt là a1; a2; a3; ...;an
Theo quy luật xây dựng dãy, ta có:
a2 - a1 = 4
a3 - a1 = 4
...
an - an - 1 = 4
Cộng n - 1 với đẳng thức trên lại, ta được: an - a1 = 4(n - 1) hay an = 4n - 1
Từ đó \(\Rightarrow\) số hạng thứ 100 của dãy là a100 = 4 . 100 - 1 = 399
b) Nhận thấy: 2015 = 4 . 504 - 1 nên số 2015 xuất hiện trong dãy trên và là phần tử thứ 504 của dãy.
a) Gọi các số hạng của dãy trên lần lượt là a1; a2; a3; ...;an
Theo quy luật xây dựng dãy, ta có:
a2 - a1 = 4
a3 - a1 = 4
...
an - an - 1 = 4
Cộng n - 1 với đẳng thức trên lại, ta được: an - a1 = 4(n - 1) hay an = 4n - 1
Từ đó ⇒⇒ số hạng thứ 100 của dãy là a100 = 4 . 100 - 1 = 399
b) Nhận thấy: 2015 = 4 . 504 - 1 nên số 2015 xuất hiện trong dãy trên và là phần tử thứ 504 của dãy.

Vì có 11 tổng mà chỉ có thể có 10 chữ số tận cùng đều là các số từ 0 , 1 ,2, …., 9 nên luôn tìm được hai tổng có chữ số tận cùng giống nhau nên hiệu của chúng là một số nguyên có tận cùng là 0 và là số chia hết cho 10.

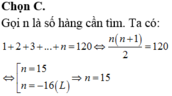
Tổng tất cả các số hạng từ hàng thứ 1 đến hàng thứ 11 là:
Chọn B.